La natura usa anche interazioni frattali multiple della spirale phi nella manifestazione di una singola forma. E’ importante notare che esiste UNA sola spirale phi che si espande all’infinito da un dato punto centrale e questa spirale può essere usata in segmenti di gruppi di 4 nodi, per creare archi discreti (e condizioni di confine) di varia grandezza di scala.
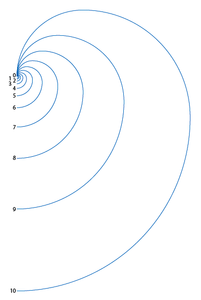
Nel caso del girasole nell’illustrazione 9, troviamo due spirali che ruotano attorno ad un centro comune in direzioni opposte (una doppia spirale). La spirale antioraria (verso il centro), possiede 34 iterazioni, mentre sono 55 quelle della spirale oraria. (Notate che 34 e 55 sono una coppia vicina di numeri nella Sequenza di Fibonacci, un esempio per capire come la natura usa il phi dalla prospettiva della Quantità). Le due spirali hanno diversi archi, tuttavia le spirali antiorarie sono molto curve e lunghe rispetto a quelle orarie. Questo avviene perchè la natura usa due scale (iterazioni frattali) della spirale phi in nodi differenti, entrambe con lo stesso punto centrale. In questo caso, usando una spirale originaria di 13 nodi, la spirale antioraria ruota attorno al nodo 4 come punto centrale (ed è la scala della condizione di confine della testa del girasole) e la spirale oraria ruota attorno al nodo 6 come punto centrale. La spirale del nodo 6 è di due iterazioni frattali del rapporto phi, più larga della spirale del nodo 4 e quindi è “meno curvata” quando le due sono centrate sullo stesso punto (anche se in effetti ha la stessa curva della spirale del nodo 4, solo più grande). Non solo la natura usa due Quantità di phi (spirali 34 e 55), ma sta anche usando due Scale (o frequenze, se viste come lunghezze d’onda) per organizzare i semi del girasole nello schema di crescita più efficiente.
Altro fenomeno significativo da notare, è che quando osserviamo la più grande condizione di confine creata dalle spirali del nodo 6 (o vortici), vediamo che si allinea molto bene con le punte esterne dei petali del girasole, mentre si estendono all’esterno.
Questo suggerisce che la natura ha combinato due iterazioni frattali del vortice phi, in uno schema di campo a doppia spirale integrato, che bilancia perfettamente il rapporto della testa di semi e dei petali, creando la disposizione più efficiente dei semi per la continuazione della riproduzione genetica.
Ecco come appare lo schema energetico dinamico di un girasole:
Quantità Phi e Numeri di Fibonacci
Come evidenziato nell’esempio del girasole, la natura spesso incorpora quantità di parti costituenti che si correlano ai numeri specifici della sequenza di Fibonacci. Vari frutti come ananas e cerimoya mostrano schemi in superficie a doppia spirale con 5 spirali orarie e 8 antiorarie o 8 orarie e 13 antiorarie, per esempio. Le tasche dei semi in una mela sono disposte come una stella a 5 punte (il pentagramma e il pentagono hanno rapporti phi ben definiti nelle proporzioni geometriche).
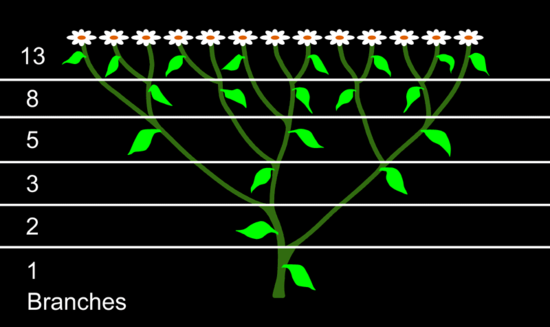
L’illustrazione 10 mostra altro esempio delle Quantità phi: un diagramma della struttura ramificata delle piante, correlata alla serie di Fibonacci
Angolazione del Cambio di Scala Phi
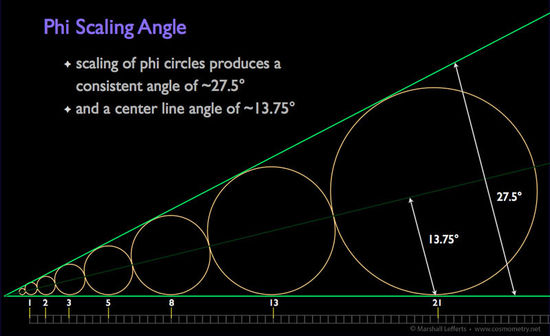
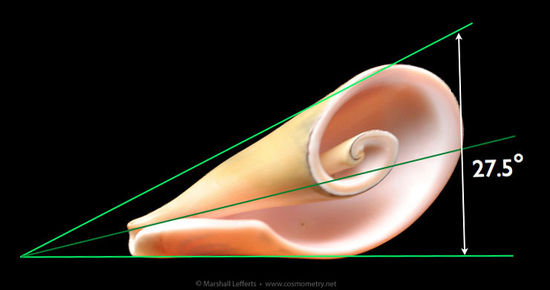
Altra caratteristica fondamentale del phi è l’angolo d’espansione o angolo del cambio di scala, inerente nel cambio di scala phi. Questo è mostrato dall’illustrazione 12, dove un gruppo di cerchi (o sfere, la forma più bilanciata simmetricamente in natura), con diametri che si espandono con i valori di Fibonacci, sono posizionati in modo tangenziale uno rispetto all’altro in linea retta. L’angolo tra la linea orizzontale in fondo ad ogni cerchio e la linea che tocca ogni punto “superiore” di superficie dei cerchi, è l’Angolo di Cambio di Scala Phi. L’angolo è approssimativamente 27.5°. L’angolo della linea centrale che interseca ogni cerchio o punto centrale della sfera è 13.75° (notiamo che è 1/10 dell’angolo di rotazione phi 137.5°)
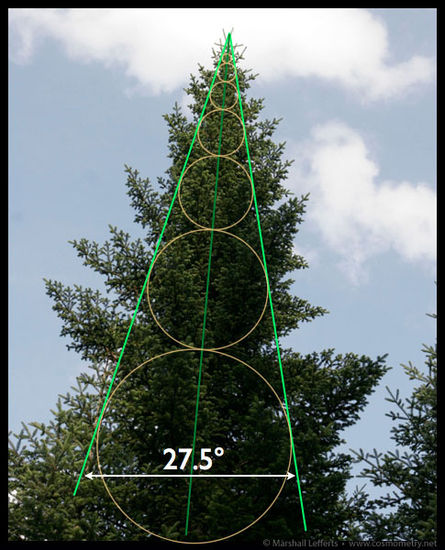
Nel prossimo esempio possiamo vedere lo stesso angolo d’espansione, ma in questo caso non è un fattore di crescita ma di efficienza. L’illustrazione 15 mostra un gruppo di pellicani che volano in formazione a V. Il pellicano in testa, attraversando la pressione delle molecole d’aria, crea un cono di vortice nel flusso, che si espande dietro di lui e riduce l’impatto del vento per gli altri pellicani. L’ottimale angolo di relazione per ottenere la minima resistenza e un volo più efficiente, è 27.5° (o 13.75° ai lati del pellicano in testa). Notate anche che questi pellicani si distanziano con un rapporto molto vicino a phi, mostrato dalla loro vicinanza alle tangenti dei cerchi.

Di seguito vediamo lo schema lasciato nella sabbia dopo la recessione di un’onda sulla costa, che mostra un'”onda” basata su questo stesso angolo. Il fenomeno è dovuto al fatto che le dinamiche di flusso dell’acqua (come con tutte le dinamiche dei fluidi, fondamentalmente) sono doppie spirali phi, allungate sulla superficie della spiaggia.

La stessa cosa vale per la corteccia di certi tipi di albero, che esibisce la stessa ovvia “onda”. Ancora, la doppia spirale phi è presente e questa volta in forma tubolare.

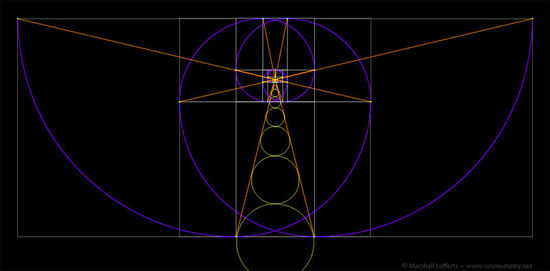
Come verifica finale dell’importanza fondamentale dell’angolo di cambio di scala phi nelle caratteristiche frattali phi, vediamo sotto l’illustrazione di due spirali phi singole, in direzione rotazionale, di colore arancio, che mostrano l’angolo differenziale. Questo angolo è l’angolo di cambio di scala phi.
Angoli di Rotazione Phi
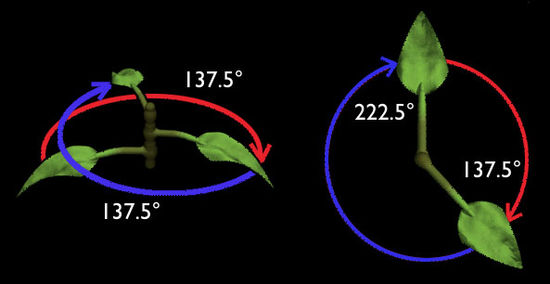
Il quarto modo per osservare la presenza del phi in natura, è come angolo di rotazione che si trova comunemente nella disposizione delle foglie nella crescita di una pianta o filotassi, come vediamo nell’illustrazione 19. Questo angolo è di 137.5° (o al contrario 222.5°) e deriva dalla divisione di 360° per phi:
360°/1.618… = ~222.5°
360° – 222.5° = 137.5°
(Notate che questo angolo di 137.5° è 10 volte più grande in magnitudine dell’angolo di cambio di scala phi della linea centrale di 13.75° che avete visto in precedenza e anche 5 volte l’angolo di cambio di scala phi di 27.5°)
L’illustrazione 20 mostra come multiple iterazioni di questo angolo di rotazione, organizzino gli steli nella disposizione più efficiente per supportare la crescita di nuove foglie e permettere alle foglie più vecchie e grandi di mantenere ancora la massima esposizione alla luce e all’aria.

Le illustrazioni vengono dal sito di Adrian O’Connor “Nature’s World” e sono una fonte eccellente di informazione sul phi e altri soggetti relativi alla geometria sacra
Sommario della Cosmometria del Phi
Ci sono molti modi per osservare la presenza del phi in natura. Ognuno di essi è una lente frattale nell’unità presente in tutta la manifestazione e ognuno ci informa sul come questa unità sia strutturata e si trasformi nell’evolvere. Questa sezione ha toccato una piccola porzione della miriade di modi per osservare questa unità e si è concentrata sulla relazione specifica del phi come fenomeno frattale-olografico e presente universalmente. Inoltre, si enfatizza lo Schema di Campo, ci sono relazioni del phi pertinenti agli altri due componenti fondamentali della cosmometria, la Forma Strutturale e Il Processo di Flusso. Questi saranno presentati in una espansione futura di questa sezione del sito Cosmometry.net.
Tradotto da Richard per Altrogiornale.org



