Spirale Phi
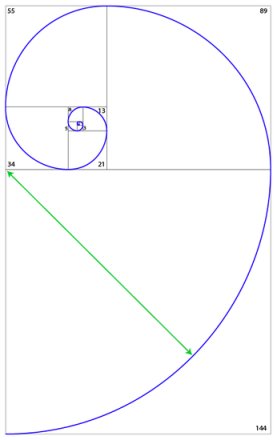
La spirale phi deriva dal semplice processo del costruire ed espandere una serie di quadrati adiacenti di dimensione crescente secondo la sequenza di Fibonacci, quindi disegnare un arco di un quarto di cerchio in ogni quadrato, con un raggio uguale alla lunghezza del lato di ogni rispettivo quadrato (vedi figura 2). Nonostante parta sempre dal punto 0 (la singolarità al centro), può espandersi infinitamente avvicinandosi con sempre maggior precisione al rapporto phi con ogni iterazione.
Nodi
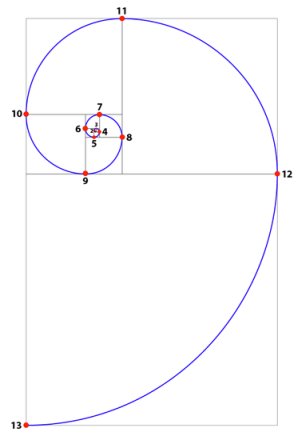
Dove la spirale risultante interseca l’angolo di ogni nuovo quadrato nell’espandersi, abbiamo un nodo. Ogni nodo è un rapporto phi sempre più lontano dal centro, lungo la spirale, rispetto a quello precedente. Partendo dal centro come zero, ogni nodo viene identificato con 1,2,3,4,5,6… (vedi figura 3). I nodi sono utili per determinare la porzione frattale della spirale phi usata dalla natura in alcuni esempi (vedi spirali phi multi-frequenza sotto).
Vortice Phi, Doppia Spirale Phi e Condizione di Confine
Vortice Phi
Duplicando e ripetendo la spirale phi in modo circolare, mantenendo un centro comune, si crea un vortice phi (in questo caso in senso orario dal centro, vedi figura 4).
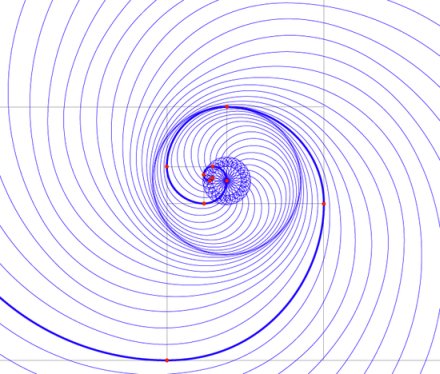
Il vortice si vede comunemente nel flussi di aria e acqua e nelle galassie, come mostrato più avanti.
Doppia Spirale Phi
Sovrapponendo due vortici di senso opposto, creiamo una doppia spirale phi (vedi figura 5). Questo è uno schema di campo fondamentale, che può essere visto come una sezione trasversale di un completo campo sferico/toroidale di energia, che troviamo nelle piante e in particolari flussi d’acqua.
Condizione di Confine
Quando creiamo un vortice o una doppia spirale phi, osserviamo un fenomeno sinergetico altrimenti non apparente con una singola spirale phi. Come vedete nella figura 5 di sopra, ad esattamente 3 nodi dal centro della doppia spirale vorticosa, è presente un cerchio distinto. Questo è il risultato della spirale phi che prima si espande dal centro verso l’esterno e poi, dopo tre archi frattali (nodi), si contrae momentaneamente su sè stessa, prima di espandersi nuovamente. Questo crea una condizione di confine, un cerchio (o sfera in 3D), che definisce un potenziale confine di superficie ed una relazione tra dentro e fuori col campo energetico. Questo confine può essere visto come limite necessario di una data entità, perchè essa possa prendere forma. Per esempio un cono di pigna mostra un ovvio schema a doppia spirale nella sua forma, con un limite nel quale ferma la sua manifestazione fisica (benchè energeticamente il suo campo si estende oltre tale limite, vedi figura 5).
Cambio di Scala Frattale-Olografico degli Schemi di Campo
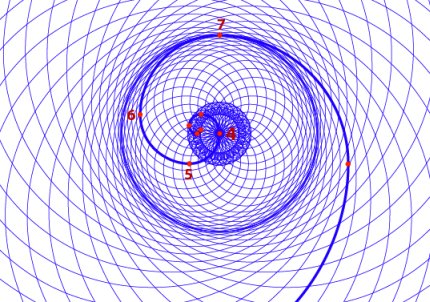
Per verificare che il rapporto phi è frattale-olografico per natura, dovrebbe essere possibile usare ogni nodo sulla spirale phi, come punto centrale della rotazione della spirale e osservare la stessa condizione di confine che nasce a 3 nodi di distanza dal centro. In effetti questo avviene. La figura 6 mostra la stessa spirale della figura 5, ma questa volta ruota attorno al Nodo 5 centrale, piuttosto che attorno al Nodo 4. Un confine appare esattamente al Nodo 8.

La figura 7 mostra tre doppie spirali, tutte create da una spirale originaria di 13 nodi e ognuna è centrata su un nodo diverso (rossa sul Nodo 9, verde sul Nodo 5 e blu sul Nodo 4)
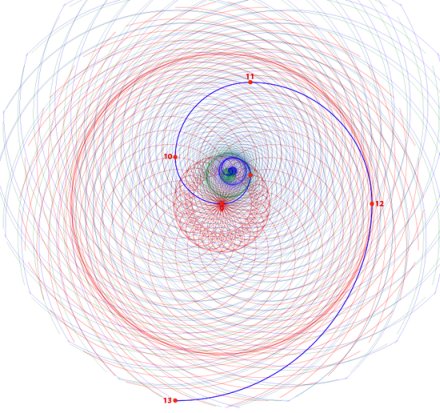
Notate come la spirale fonte sia in comune con le altre tre. Se tracciate il percorso della spirale fonte, esso è presente in ogni doppia spirale e continuo in sè, quindi olografico. Chiaramente, ogni iterazione dello schema a doppia spirale, è più grande o più piccola di quella vicina, secondo il rapporto phi, quindi frattale.
Il vortice e la doppia spirale phi, sono chiaramente forme visibili in natura. Eccovi alcuni esempi con le spirali in evidenza:
Vortice Phi in Aerodinamica: un turbine d’aria crea un vortice phi, reso visibile dal fumogeno rosso.
Vortice Phi nell’Acqua: un tornado sull’acqua crea un vortice phi in superficie
Girasole: un classico esempio della doppia spirale phi è visibile nella testa del girasole e di molti altri fiori e piante
Vortice Phi nella Galassia: nella scala universale, le strutture più grandi del cosmo esibiscono il rapporto phi, come nella spirale della galassia
Le doppie spirali si vedono anche in molti cactus e fiori, nella corteccia di tronchi e rami e nelle ondulazioni della sabbia mossa dalle onde marine. Esse sono spesso distorte, compresse o allungate o tubolari come nei tronchi degli alberi.
Doppia Spirale nella Sabbia: quando un’onda si ritira, lo fa seguendo una doppia spirale e lasciando uno schema sulla sabbia.
Doppia Spirale nella Corteccia degli Alberi: la doppia spirale si conforma anche ad una struttura “tubolare”, come vediamo negli alberi.
Tradotto da Richard per Altrogiornale.org








