(Intervista a Fausto Intilla – www.oloscience.com)

In questa intervista a Fausto Intilla (saggista/divulgatore scientifico, noto per i suoi interessi in ogni ambito del sapere umano), Altrogiornale ha voluto riesplorare alcuni temi piuttosto controversi, nell’ambito delle scienze di confine, ancora molto dibattuti tra scienziati che si occupano di scienze dure ma sempre attenti a tutto ciò che pian piano sta emergendo, attraverso una maggiore comprensione dei fenomeni dinamici che governano la realtà apparente a noi circostante. La famosa teoria di Rupert Sheldrake sui campi morfici (o morfogenetici), fa indubbiamente parte di determinate speculazioni ai confini tra la biologia molecolare e il regno della meccanica quantistica; dove a prevalere, in tale contesto, è la teoria dell’informazione intesa come fonte primaria di ogni realtà fisica e da cui in futuro dovrebbero trarre origine (con opportune modifiche essenziali), parafrasando Anton Zeilinger, tutte le teorie oggi note della fisica quantistica. Diamo dunque il benvenuto al diretto interessato e cerchiamo di capire, attraverso alcune semplici domande, quale potrebbe essere il filo conduttore che lega il mondo della biologia molecolare a quello della fisica quantistica.

A.G.: Buongiorno Fausto e bentrovato. Assumendo che molti lettori siano già a conoscenza, a grandi linee, della teoria speculativa di Sheldrake sui campi morfici (internet è ormai pieno di blog che la citano e ne spiegano i principi fondamentali), da quali elementi o basi concettuali è possibile partire, a tuo avviso, per andare un pochino più a fondo nell’argomento?
F.I.: Indubbiamente, dal concetto fisico-matematico di attrattore. Prendiamo ad esempio il famoso attrattore strano di Lorenz. Si immagini lo stato iniziale di un sistema (ad esempio quello dell’atmosfera in convezione) come rappresentato da un punto P e il suo spostamento temporale; esso ha luogo secondo una linea curva tracciata dal computer. In un grafico tridimensionale (con origine in O e i tre assi x, y e z), il punto P prende l’avvio presso l’origine O delle coordinate, poi gira attorno all’ “orecchio” destro dell’attrattore, passa varie volte attorno all’orecchio sinistro, gira due volte attorno all’orecchio destro e così via. Se la posizione iniziale di P nei pressi di O venisse modificata anche solo leggermente (addirittura con una modifica di posizione non visibile ad occhio nudo), la figura dell’attrattore creata al computer verrebbe totalmente sconvolta/modificata! Ciò è dovuto al fatto che l’evoluzione temporale della figura rappresentante l’attrattore in questione, dipende in modo molto sensibile dalle condizioni iniziali.

A.G.: Ma cosa sarebbe, dunque, in sintesi, un attrattore?
F.I.: In sintesi è l’insieme su cui si muove il punto P che rappresenta lo stato di un sistema dinamico deterministico, quando si attenda abbastanza a lungo. In sostanza, l’attrattore descrive la situazione di regime, dopo la sparizione dei fenomeni transitori. Tuttavia, affinché tale definizione abbia un senso, è importante che le forze esterne che agiscono sul sistema, siano indipendenti dal tempo. È importante inoltre che ci si interessi a sistemi fisici “dissipativi” (ossia a sistemi che dissipino energia in calore; i fluidi viscosi, ad esempio, dissipano l’energia meccanica per attrito interno). È la dissipazione a far sparire i fenomeni transitori ed è anche a causa sua che nello spazio di dimensione infinita che rappresenta un sistema, vi sia solo un “piccolo insieme” davvero interessante: l’attrattore.

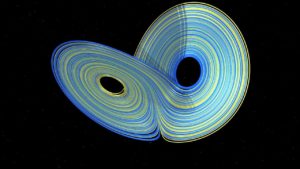
A.G.: Ovviamente è tutto molto interessante; tuttavia, dove ci porta il concetto stesso di attrattore, se il fine ultimo è quello di comprendere i meccanismi intrinseci di tutte le dinamiche biomolecolari, ovvero l’origine, la matrice di tutte le forme della natura e soprattutto della vita?
F.I.: Ottima domanda. Ebbene in molti modelli di cambiamento, il fine (o l’obiettivo) è visto implicitamente come un attrattore, per analogia con la gravità. In chimica, per esempio, si costruiscono modelli dei processi di cambiamento sotto forma di pozzi di potenziale. Un sistema è attratto verso il punto più basso; ovvero quello in cui l’energia è minima. Nei modelli matematici della dinamica, scopi (od obiettivi) sono rappresentati da attrattori (che a loro volta si trovano in “bacini di attrazione”). Ora, si tenga presente che già più di mezzo secolo fa, il biologo Conrad Waddington descriveva la natura volta al fine dello sviluppo embrionale, in termini di attrattori in un “paesaggio epigenetico”; dove ciascuno dei punti terminali rappresenta un organo (ad esempio un occhio oppure un polmone), verso il quale una parte dell’embrione si sta sviluppando. Per certi versi, si potrebbe dunque affermare che i sistemi in via di sviluppo, vengono attratti verso i loro scopi finali; in tale contesto quindi, non vengono solo “spinti dal passato”, ma vengono altresì “trainati dal loro futuro”. Negli anni Settanta e Ottanta, il matematico francese René Thom ha sviluppato ulteriormente le teorie di Waddington, utilizzando modelli topologici dinamici. Mentre i modelli di Waddington erano semplici grafici, quelli di Thom erano molto più tecnici e facevano leva su una branca della matematica chiamata: topologia differenziale (ovvero lo studio delle superfici continue e delle loro trasformazioni in oggetti con proprietà spaziali differenti).

Anche i suoi modelli erano dinamici, nel senso tecnico della dinamica come studio del cambiamento nel tempo e si collocavano in spazi di fasi multidimensionali. Thom utilizzava la topologia differenziale per creare modelli dei processi di sviluppo (in termini di attrattori), in campi morfogenetici atti a “trainare” le strutture in via di sviluppo (nello specifico parti di organismi vegetali, come ad esempio una foglia; oppure di organismi animali, come ad esempio un rene). Inoltre, cosa assai importante, gli attrattori in questi campi contribuivano a spiegare la rigenerazione di strutture perdute o danneggiate.

A.G.: Qualcuno a questo punto potrebbe chiedersi se il “trascinamento” dei processi verso gli attrattori, sia un fenomeno limitato solo agli organismi viventi macroscopici. Come stanno le cose in tal senso? Vi sono dei vincoli o dei limiti a tale fenomeno, per ora sperimentalmente non dimostrabile?
F.I.: Attenzione, non è vero che tale fenomeno non possa essere osservato in natura. Pensiamo ad esempio allo sviluppo di un uovo di libellula dopo che ne è stata distrutta mezza parte. Normalmente la parte posteriore dell’uovo origina la parte posteriore dell’embrione; ma se la parte anteriore dell’uovo viene distrutta, la parte posteriore dà origine a un embrione più piccolo, ma completo. Analogamente, nella rigenerazione, si può ripristinare un organismo completo da una sua parte; si pensi ad esempio a come un rametto di salice tagliato, possa dare origine a un nuovo albero. Se si taglia a pezzi un platelminta (o vermi piatti), ogni frammento può rigenerare un animale completo. Anche le singole cellule hanno stupefacenti capacità rigenerative. L’Acetabularia è un’alga unicellulare verde, lunga circa cinque centimetri, con tre parti principali: strutture simili a radici, i rizoidi (che le permettono di attaccarsi a una roccia), un fusto e un “cappello” del diametro di circa un centimetro. Questa grandissima cellula ha un unico nucleo, in uno dei rizoidi. Con la crescita, il fusto si allunga e l’alga forma una serie di ciuffi di peli che poi cadono e infine forma il cappello.

Se si recide il cappello spezzando il fusto in due, dopo che la ferita si è rimarginata si forma una nuova punta e il fusto forma una serie di ciuffi di peli e quindi un nuovo cappello, seguendo uno schema analogo a quello di una crescita normale (e questo può verificarsi più volte, se si continua a recidere il cappello). L’ipotesi che si fa di solito è che i geni in qualche modo controllino o programmino lo sviluppo della forma; come se il nucleo, che contiene i geni, fosse una sorta di cervello che controlla la cellula. Ma l’Acetabularia mostra che la morfogenesi può verificarsi anche senza geni; ciò ovviamente depone a favore dell’evidenza che la morfogenesi è volta a uno scopo ben preciso, andando verso un attrattore morfico anche in assenza di geni. Infine, la cosa davvero sorprendente è che il “trascinamento” dei processi verso gli attrattori, non è un fenomeno limitato agli organismi viventi. Anche la formazione di molecole è un tipo di morfogenesi; infatti le loro forme possono essere rappresentate da attrattori che giacciono sul fondo di pozzi di potenziale.

Le molecole sono stabili perché sono strutture di energia minima; se vengono perturbate e allontanate dal fondo del pozzo, tendono subito a tornarvi. Nel caso di molecole semplici come l’anidride carbonica, si ha una struttura di energia minima semplice; nel caso invece di molecole grandi e complesse come le proteine, il numero di strutture possibili diventa infinitamente grande. Infatti è risaputo che i calcoli per prevedere la struttura tridimensionale delle proteine (a partire dalla successione lineare degli amminoacidi per cui codifica il DNA), portano a un numero incredibilmente elevato di soluzioni possibili (ad esempio, se i singoli residui di una catena polipeptidica non ripiegata potessero avere due soli stati, una stima eseguita per difetto mostra che il numero di possibili conformazioni generate in modo casuale, sarebbe di 10^45 per una catena di 150 amminoacidi residui!) .

Tuttavia, in natura tale problema viene risolto in modo piuttosto semplice; infatti, in risposta a determinate interazioni locali, le catene peptidiche sembrerebbero dirigersi lungo una serie di possibili cammini a bassa energia, il cui numero è relativamente piccolo, forse passando attraverso stati intermedi specifici, verso una ben determinata e specifica conformazione di minima energia libera. Se ne deduce quindi, in ultima analisi, che analogamente alla morfogenesi relativa agli organismi viventi macroscopici, anche la morfogenesi chimica è volta a uno scopo ben preciso.

A.G.: Siamo dunque giunti al nesso, da quanto ci è dato di capire, tra attrattori e campi morfogenetici. Alcune domande tuttavia, a questo punto sorgono quasi spontanee. Ma, gli attrattori nei campi morfogenetici, rappresentano soltanto degli enti matematici astratti? Oppure i campi morfogenetici esercitano realmente un influsso causale, attirando gli organismi verso i loro obiettivi? È possibile che esista un altro tipo di causalità in natura (evidentemente nascosta e quindi non apparente), al di fuori delle forze e dei campi già noti ai fisici?
F.I.: La causalità da fini virtuali o attrattori che operano “a ritroso” nel tempo si adatta bene alla distinzione temporale di Whitehead tra mente e materia, con le cause mentali che operano “a ritroso” verso il passato. La causalità mentale fluisce a ritroso dal regno delle possibilità nel futuro virtuale e interagisce nel presente con l’energia che fluisce in avanti dal passato e i risultati sono gli eventi fisici osservabili. La spinta dell’energia dal passato e il traino dai futuri virtuali si sovrappongono nel presente.

AG: Ma come è possibile che traguardi virtuali esercitino un influsso causale, operando “a ritroso” nel tempo? Questo influsso causale è confinato al regno virtuale, a ciò che è in potenza anziché a ciò che è in atto? Oppure ci può essere anche un influsso degli eventi futuri, verso quelli che li precedono?
F.I.: Quasi tutti danno per scontato che la causalità “inversa” nel tempo sia scientificamente impossibile; ma, sorprendentemente, la maggior parte delle leggi della fisica è reversibile (ovvero, funzionano bene dal passato al futuro, come dal futuro al passato). Nelle equazioni classiche di Maxwell, ci sono due risposte che descrivono il movimento delle onde luminose: in una le onde si muovono alla velocità della luce dal presente al futuro (come si intende convenzionalmente la causalità), ma nell’altra le onde si muovono dal presente verso il passato alla velocità della luce (nel senso inverso a quello della causalità ordinaria). Queste onde che procedono a ritroso nel tempo, sono chiamate “onde avanzate” e comportano la possibilità di influssi che operano a ritroso nel tempo. Le onde avanzate fanno parte della matematica dell’elettromagnetismo, ma in genere in fisica classica vengono ignorate perché ritenute “non fisiche”. Tuttavia, qualche interpretazione della meccanica quantistica ammette la possibilità che esistano “influssi fisici” che operano a ritroso nel tempo; ovvero, in altri termini, influssi causali dal futuro.

Ad esempio nell’interpretazione di Feynman, si può intendere un positrone (ovvero l’antiparticella dell’elettrone), come un elettrone che si sposta “a ritroso” nel tempo. Parallelamente, nell’interpretazione “transazionale” della meccanica quantistica (ideata da John Cramer), i processi quantistici sono visti come onde stazionarie fra emittente e assorbente; con le onde che procedono nel senso del tempo, in moto dall’emittente all’assorbente, e quelle che procedono in senso inverso, in moto dall’assorbente all’emittente. Infine, vi è ancora un altro modo di considerare i flussi bidirezionali nel tempo nella MQ, ed è quello proposto dal fisico Yakir Aharonov. Invece di descrivere i processi quantistici soltanto come propagantisi in avanti nel tempo, egli li descrive anche come propagantisi a ritroso nel tempo.

In sostanza, in tale modello l’evoluzione del tempo è vista come un insieme di correlazioni fra stati quantistici (in avanti e a ritroso), in momenti adiacenti. Chiaramente, nel momento in cui entra in crisi il concetto stesso di “freccia del tempo”, si entra prepotentemente nel campo della fisica quantistica. Oggigiorno, la teoria più accreditata in tale ambito scientifico, atta a descrivere nel migliore dei modi ogni forma della realtà fisica a noi circostante, è indubbiamente la teoria quantistica dei campi (QFT). Si è dunque passati dall’idea iniziale che non possa esistere alcuno spazio, vuoto di campo (come Einstein ebbe a dire già agli inizi del secolo scorso), all’idea che tutto, fondamentalmente, è campo (materia “solida” compresa, ma a livelli di “densità” infinitamente grandi; sul fatto che la massa non sia altro che una forma complessa di energia, ormai nessuno ha più dubbi. Tuttavia, sul fatto che l’energia non sia altro che una forma complessa di informazione, il dibattito è ancora aperto). In sintesi dunque, se tutto è campo e tutto è, fondamentalmente, informazione, chiaramente la teoria di Sheldrake sui campi morfogenetici (intesi come campi di informazione dinamica e auto-organizzanti), a mio avviso non è affatto da sottovalutare o da escludersi a priori. In base al limite olografico, anche un piccolissimo frammento di materia, in teoria, può “immagazzinare” una quantità infinitamente grande di informazione.

Si pensi che un solo centimetro cubo di materia, può contenere, almeno in teoria, fino a 10^66 bit di informazione; più o meno lo stesso numero di atomi contenuti in un’intera galassia! Si tratta quindi di un numero finito, non infinito. Si arriva dunque al concetto che l’informazione abbia una vera e propria “natura fisica”. È possibile infatti registrare un qubit su un atomo, manipolandone lo spin, la posizione, oppure qualche altro dettaglio fisico; dove ogni qubit registrato deve riflettersi nelle proprietà complessive, intese ovviamente come stati quantistici dell’atomo stesso. Da ciò si arriva facilmente alla conclusione che una data massa, può contenere solo una certa quantità di informazione; questo poiché qualsiasi oggetto materiale deve necessariamente trovarsi in uno degli stati quantistici che gli sono permessi e il cui numero è finito. In altri termini, un oggetto può avere solo un numero finito di funzioni d’onda quantistiche; ovvero la funzione d’onda che “racchiude” tutta l’informazione di tale oggetto (sia essa accessibile o meno).

Ma l’aspetto più interessante di tutto ciò, che occorre assolutamente sottolineare e ricordare (per poter afferrare intuitivamente il nesso con la teoria di Sheldrake sui campi morfici), è che nessun oggetto esistente e concepibile in natura, può trovarsi “scollegato” dalla realtà ad esso circostante (dove tutto è campo, non può esserci frammentazione; Unus Mundus, per dirla con un tocco di scolasticismo).

A.G.: Dopo tutte queste considerazioni che hanno quasi dell’incredibile, è proprio il caso di affermarlo senza alcuna ombra di dubbio: La realtà, come al solito, è ben più complessa di come normalmente ci appare! Grazie di cuore per la tua disponibilità, Fausto. Un caro saluto a nome di tutta la redazione di Altrogiornale.org. Alla prossima!
F.I.: Grazie a voi, a presto!