In questo lavoro vediamo come, attraverso un  percorso essenzialmente matematico, si potrà arrivare in futuro alla T.O.E, nota come Teoria del Tutto, attraverso i numeri primi, i numeri primi supersingolari, i numeri di Fibonacci (un percorso alternativo sarebbe quello attraverso la teoria di gravità a loop, ma con meno matematica). Alla cosiddetta TOE (acronimo di Theory Of Everything), si potrebbe benissimo arrivare dalle stringhe (e relative teorie), e prima ancora anche dalla Teoria dei Numeri in generale e dei numeri primi in particolare:
numeri primi di Chen, i numeri primi supersingolari come fattori degli ordini dei Gruppi sporadici di Lie, ma anche i numeri di Grassmann, i numeri di Fibonacci, ecc. Qualcuno però non è molto d’accordo con la via delle stringhe; per esempio, il Prof. Roberto Battiston dell’Università di Perugia, che sulla rivista “Le Scienze” di gennaio 2009, nel suo articolo “I nodi della teoria delle stringhe”, tra l’altro scrive (pag. 21, rubrica “Astri e
particelle”):

“All’inizio sembrò addirittura che ci fossero particolarissimi gruppi di simmetria, come per esempio E8 e Su(32), in grado di risolvere importanti problemi teorici candidandosi ad essere il gruppo di simmetria della teoria della superstringa. Il gruppo di simmetria E8 è chiamato “gruppo eccezionale di Lie”: esso rappresenta le possibili simmetrie nelle trasformazioni in uno spazio a 248 dimensioni, e non c’è da stupirsi del fatto che da un punto di vista matematico sia un oggetto tanto complesso da risultare oscuro anche agli esperti. Nel 1995 Witten introdusse un ulteriore sviluppo, la Teoria – M, anch’essa affascinante da un punto di vista matematico ed estetico ma altrettanto intrattabile dal punto di vista dei calcoli e per nulla predittivo dal punto di vista fisico. Oggi sappiamo che di possibili stati del vuoto, e, conseguentemente, di Teorie – M ce ne possono essere un numero smisurato, dell’ordine di 10^500. Anche per questo motivo un numero crescente di fisici teorici ha iniziato a prendere le distanze dalle superstringhe, soprattutto considerando l’assoluta mancanza di verificabilità sperimentali di queste teorie, quasi si trattasse di metafisica…
A distanza di trent’anni dai primi lavori di Schwarz, Green e Witten, l’idea delle superstringhe ha monopolizzato l’attività di ricerca in campo teorico, senza riuscire a fornire una qualsiasi predizione falsificabile. L’idea che la bellezza di una teoria sia collegata in modo profondo alla verità scientifica ha permesso ad Einstein di formulare la teoria generale della relatività. Nel caso delle superstringhe, è possibile che questo schema abbia fuorviato un’intera generazione di fisici teorici, e che occorra oggi battere nuove strade per spiegare le questioni rimaste aperte nella fisica delle interazioni fondamentali”

Fin qui il Prof. Battiston. Ma il Prof. Ian Stewart, insegnante di matematica alla Warwich University, e apprezzato divulgatore, è di tutt’altro avviso, che espone nel suo recente libro “L’eleganza della verità” (Einaudi), a pag. 295, parlando anche dello stesso gruppo di simmetria a cui si riferisce anche il prof. Battiston:

“Per molto tempo gli ottonioni rimasero un’innocua curiosità, perchè contrariamente ai quaternioni non avevano alcuna interpretazione geometrica o applicazione ad altre scienze: Anche all’interno della matematica caddero nell’oblio. Fino a quando un giorno si è scoperto che sono all’origine delle più bizzarre strutture algebriche in circolazione: i cinque gruppi eccezionali di Lie classificati da Killing, G2, F4, E6, E7 ed E8.. Inoltre, il più grande di questi oggetti, E8,salta fuori non una ma due volte nel gruppo di simmetria alla base della teoria delle stringhe in dieci dimensioni, che ha molte proprietà utili ed inconsuete ed è una delle
candidate più autorevoli al ruolo di teoria del Tutto.

Se come Dirac pensiamo che l’universo affonda le radici nella matematica,
potremmo azzardarci ad affermare che una Teoria del Tutto plausibile esiste perché esiste E8, che a sua volta esiste perché esistono gli ottonioni. Dal punto di vista filosofico, si apre una stuzzicante possibilità: la struttura di base dell’Universo in cui abitiamo e che sappiamo essere speciale in molti modi, è individuata in modo particolare nella sua relazione con una sola struttura matematica, cioè gli ottonioni.
“Bellezza e verità, verità bellezza” (concetto richiamato anche dal prof.
Battiston, n.d.A.A.). I pitagorici e i platonici avrebbero gradito molto questo
possibile ruolo centrale di una struttura matematica nel sistema del mondo. Gli ottonioni hanno una bellezza conturbante e surreale, che Dirac avrebbe presa come forte indizio del fatto che la teoria delle stringhe a dieci dimensioni fosse vera. O, se per un caso sfortunato si fosse rilevata falsa, del fatto che fosse comunque più interessante della verità, qualunque essa fosse.

Ma abbiamo imparato a nostre spese che ci sono teorie eleganti e non necessariamente vere; dunque, prima del verdetto finale sulle superstringhe, dobbiamo ricordarci di essere nel campo delle pure speculazioni. Qualunque risulterà essere il suo ruolo in fisica, la cassa in cui sono racchiusi gli ottonioni si è rivelata un vero tesoro per i matematici.
E poi ancora, a pag. 305:
Se non ci fossero stati gli ottonioni, la storia dei gruppi di Lie sarebbe stata
più semplice, come Killing sperava all’inizio della sua impresa, ma molto meno interessante. A noi mortali non è data scelta, visto che ottonioni e compagnia sono lì e ci restano. Addirittura, forse da loro dipende in qualche misterioso modo l’esistenza stessa dell’universo.
La nuova candidata di moda, la M-teoria, prevede uno spazio tempo a undici dimensioni. Per far si che corrispondano alle quattro da noi percepite, dobbiamo prendere le rimanenti sette ed arrotolarle strettamente. E come si fa dal punto di vista tecnico questa operazione? Grazie a G2, il gruppo di Lie eccezionale, cioè il gruppo di simmetria degli ottonioni. Ancora loro: non più curioso relitto dell’era vittoriana, ma poderoso indizio verso una probabile Teoria del Tutto: verso un mondo
ottonionico.”

Quindi, sarebbe consigliabile una maggiore prudenza nel “liquidare” la teoria delle stringhe come poco adatta per fare da base per la TOE. Le previsioni verificabili? Potrebbero arrivare in seguito, basta aspettare ancora un pò (vedi Nota 1). Gli ottonioni sono particolari numeri complessi. I numeri complessi più semplici sono legati alle teorie di stringa dalla funzione zeta di Riemann, e della cui ipotesi RH siamo certi che sia vera (Rif.1 sull’equivalenza di Lagarias RH1 = RH, con RH1 equivalente alla RH ma basata sulla funzione σ(n), somma dei divisori di n, anziché sui numeri primi). Oltre che con i numeri complessi e i numeri primi, le teorie delle stringhe hanno, com’è noto, relazioni matematiche anche con i gruppi di Lie, che a loro volta sono anch’essi connessi con i numeri primi: i fattori del loro ordine (numero di elementi) sono anche numeri primi di Chen, detti anche numeri primi supersingolari (e sono in tutto quindici) nel caso del cosiddetto gruppo mostro, o “Monster Group”. Gli stessi gruppi di Lie, essendo anche gruppi di simmetria, sono pur gruppi di permutazioni di n elementi, e quindi sono connessi ai numeri fattoriali n! e   contemporaneamente anche ai numeri di Fibonacci, con la relazione da noi recentemente scoperta:

L=k · n! + k’ · F(1)
dove L è l’ordine di un qualsiasi gruppo di Lie, ed F un numero di Fibonacci. Per esempio, per G2=14, ed altri gruppi,
14=3! + 1 x 8=6 + 8
52=6 x 3! + 2 x 8=6 x 6 + 16=36 + 16
ma anche 52 – 24=28=2 x 14 (gruppo G2) dove 24=4!

133=5! + 1 x 13=120 + 13

248=2 x 5! + 1 x 8=2 x120 + 8=240 + 8

ma anche 248-144=104=2 x 52 gruppo di Lie F4 ..e così via.

I numeri di Fibonacci sono peraltro anche legati ai numeri D di dimensioni coinvolte nelle teorie di stringa, con la relazione D=2F, infatti D=2, 4, 6, 10,
16, 26 sono esattamente il doppio di F=1, 2, 3, 5, 8, 13 che sono numeri di Fibonacci (Rif. 2). Semplici coincidenze?
Concludendo, i gruppi di Lie sono connessi:
a) ai numeri complessi tramite gli ottonioni;
b) ai numeri primi tramite i numeri primi di Chen e quindi anche supersingolari;
c) ai numeri fattoriali tramite le permutazioni;
d) ai numeri di Fibonacci tramite la nostra relazione sopra accennata (Rif.3, ultimi lavori del Dott. Michele Nardelli o in comune).

Quindi tutti questi numeri, tramite i gruppi di Lie, sono connessi anche alle teorie di stringa, che vi affonda le sue radici ( con grande soddisfazione dei pitagorici e platonici moderni, noi compresi); e qualche particolare teoria di
stringa potrebbe così essere la struttura portante di una futura possibile TOE. A questo punto è doveroso affermare che anche la strada delle teorie di stringhe o delle superstringhe merita di essere battuta, magari insieme ad altre possibili strade (supergravità o altre), ma non deve essere assolutamente trascurata nè tanto meno abbandonata anche perché entrambe le strade possono essere alla fine le facce di una stessa medaglia. (Rif. 4, anche per un lavoro del Dott. Nardelli ancora in corso)
La conclusione a cui arriviamo è che ci sembra ancora presto per liquidare frettolosamente le teorie di stringa in relazione con possibili T.O.E.

Nota 1:
Nel riferimento 7. la teoria di stringa su cui si basa la T.O.E di A.Garrett Lisi sembra essere la teoria denominata HE a 10 dimensioni (vedi “Teoria delle stringhe” su Wikipedia) così sintetizzata: “Supersimmetria tra forze e materia, solo stringhe chiuse, eterotiche, cioè le stringhe che si muovono verso destra differiscono da quelle che si muovono a sinistra, nessun tachione, gruppo simmetrico E8 x E8“

Nota 2:
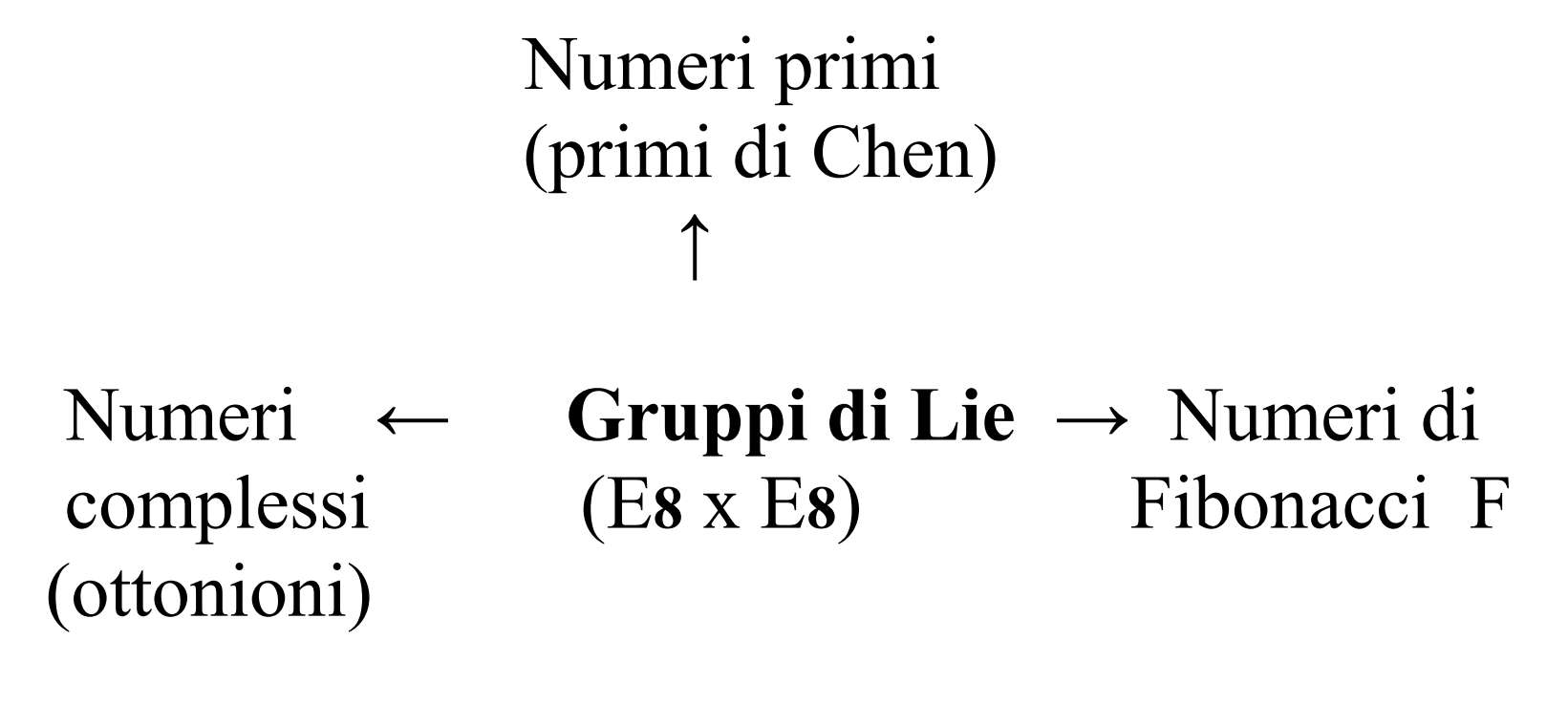
Schema generale delle relazioni tra numeri e gruppi di Lie:

V

Fattoriali n! (permutazioni)

Con i gruppi di Lie al centro delle teorie di stringa e in prospettiva, anche delle possibili T.O.E basate su tali teorie. Per le T.O.E basate sulla gravità quantistica ad anelli (loop), vedi successiva seconda parte.

Riportiamo anche, per completezza di questo lavoro, le altre due teorie candidate a TOE, oltre alle teorie di stringa viste nella I PARTE. Dal libro di Ian Stewart, op. cit., pag. 287. “Non vorrei dare l’impressione che le superstringhe siano le uniche candidate alla carica di grande unificatore tra quanti e relatività. Esistono varie proposte concorrenti, che però soffrono tutti dello stesso male: la mancanza di supporto sperimentale. Una di queste, la geometria non commutativa, è frutto della fervida mente del matematico francese Alain Connes e si basa su un concetto inedito della geometria spaziale. Gran parte delle teorie di unificazione partono dall’idea che lo spazio-tempo sia una qualche espansione del modello relativistico di Einstein e cercano di farci entrare in qualche modo le particelle elementari. Connes fa l’esatto contrario: parte da una struttura chiamata spazio non commutativo che contiene tutti i gruppi di simmetria che compaiono nel Modello Standard e ne deduce certe caratteristiche simili alla relatività. La matematica di questi spazi affonda le sue radici nelle idee di Hamilton, tra cui i quaternioni, fortemente generalizzate e modificate. Anche questa proposta, comunque, non può fare a meno dei gruppi di Lie.

Commento: anche questa candidata T.O.E come scrive Stewart, contiene la simmetria e quindi anche i numeri fattoriali, gli ottonioni e quindi i numeri complessi, oltre ai Gruppi di Lie e i numeri primi connessi (numeri primi di
Chen come fattori dei loro ordini). Mancano ancora i numeri di Fibonacci, da noi proposti con vari e recenti lavori contenenti la relazione (1), la sezione aurea e il numero aureo.

“Un’altra candidata affascinante è la gravità quantistica ad anelli spesso citata col nome inglese, loop quantum gravity. Tutto è partito negli anni Ottanta da un lavoro di Abhay Ashketar, che si è messo a verificare quale forma avrebbero assunto le equazioni di Einstein in uno spazio “sgranato”.
Queste idee sono portate avanti da Lee Smolin e Carlo Rovelli, che hanno proposto un modello di spazio simile a una cotta ferrata come quella indossate dai guerrieri medievali, le cui maglie hanno un diametro di circa 10-15 metri. La struttura fine di questo complesso di anelli e giunture può diventare estremamente complicata, sino a formare nodi e attorcigliarsi. In un primo momento, non era chiaro il significato fisico di queste  configurazioni. Nel 2004 Sundance Bilson-Thompson ha scoperto che in alcuni casi questi intrecci riflettono perfettamente il comportamento dei quark. La carica elettrica si può ricavare sulla base della topologia della “treccia” associata e le regole per la combinazione derivano da semplici operazioni geometriche sulle trecce stesse…
Il metodo è ancora in fase embrionale ma sembra in grado di produrre parte delle particelle presenti nel Modello Standard. E’ l’ultima di una serie di speculazioni che vedono la materia (le particelle, in questo caso) nascere come conseguenza delle singolarità presenti nello spazio, come nodi, perturbazioni e altre strutture più complicate, luoghi in cui il panorama cessa di presentarsi come liscio e regolare. Se Bilson-Thompson ha visto giusto, la materia non è altro che un intreccio nella trama dello spazio-tempo. I matematici studiano da tempo la topologia delle trecce e sanno bene che anche queste formano un gruppo, il gruppo delle trecce, in cui la moltiplicazione è fatta unendo i cappi dei due membri (un po’ come la moltiplicazione di permutazioni che abbiamo visto parlando di Ruffini).
Ancora una volta la fisica sembra costruire ipotesi a partire da una scoperta matematica precedente, studiata solo perché sembrava interessante. E, ancora una volta, la simmetria gioca un ruolo molto interessante”.

Commento: in questa teoria, sono invece presenti solo le simmetrie (e quindi permutazioni e numeri fattoriali), ma almeno non direttamente, non vi sono coinvolti gli altri numeri visti nelle teorie di stringa: numeri primi, complessi, di Fibonacci. Circa invece un universo ciclico basato sulle stringhe, (pag. 289 – 290), Stewart così conclude il capitolo quattordicesimo, pag.290: “nel 2006 Paul Steinhardt e Neil Turok hanno proposto una variazione dell’idea del tunnel: un universo ciclico che si espande dopo un Big Bang e si contrae in un Big Crunch, con un periodo di mille miliardi di anni o giù di lì. In questo modello, l’energia del vuoto diminuisce ad ogni ciclo, in modo che alla fine abbia un valore abbastanza piccolo ma non nullo. In entrambe le versioni della storia, un universo con energia del vuoto “giusta” deve esistere per un periodo molto lungo. Le condizioni favorevoli alla vita, dunque, durano abbastanza da permettere l’evoluzione di una creatura intelligente in grado di domandarsi che cosa ci stia facendo lì”.

Commento: una vera T.O.E dovrebbe comprendere sia un eventuale universo ciclico, sia le condizioni per l’evoluzione di una qualche forma di vita, specialmente se di tipo “intelligente” e qui la faccenda si connette al
fenomeno “coscienza”. Circa tale ipotizzato universo ciclico, nel recente articolo su “Il Sole 24 Ore” (“L’universo è come un “loop””), l’Autore Carlo Rovelli, fisico, scrive:
“ …La struttura di questi atomi di spazio ricorda un tessuto formato da anelli (i “loop”) intrecciati tra di loro,da cui il nome della teoria. E’ stata concepita alla fine degli anni Ottanta, combinando le due maggiori scoperte della fisica teorica del XX secolo: la relatività generale di Einstein e la meccanica quantistica. Da poco, si è capito che le equazioni messe a punto per la teoria dei loop si possono applicare alla dinamica del Big Bang”.

A differenza di quelle di quelle della relatività generale o di altre teorie, continuano a funzionare anche quando si usino per descrivere l’inizio dell’universo. Cresciuto negli ultimi anni, il campo di ricerca – la cosmologia quantistica dei loop – ha ottenuto un risultato spettacolare: dalle equazioni, emerge la possibilità che il Big Bang possa essere il risultato di un gigantesco “rimbalzo”, dopo una precedente fase in cui un universo è collassato su se stesso, sotto il peso della sua forza di gravità.
Quando questo universo è collassato fino a ridursi in un singolo atomo di spazio, la temperatura è diventata così alta che lo spazio e il tempo stessi, così come li conosciamo attualmente, si sarebbero fusi in una nube di probabilità quantistica, per poi riemergere in una violentissima espansione. Secondo questa ipotesi il nostro universo, attualmente in espansione, starebbe tuttora rimbalzando.”

Commento: tale rimbalzo potrebbe anche essere legato alle teorie di stringa, quale possibile “connessione” con la teoria dei loop. Uno di noi (M.Nardelli) scriverà un articolo sull’argomento per ipotizzare una forma equivalente di universo ciclico.

Nota 1 alla seconda parte

Circa l’attuale mancanza di previsioni e/o prove sperimentali nelle teorie di stringa, così scrive Ian Stewart nel suo libro, op. cit., pag. 285-286: “Oggi si registra una certa reazione contro la teoria delle stringhe, non tanto perché si crede che sia sbagliata, ma perché non c’è modo di sapere se sia giusta. Molti fisici autorevoli, soprattutto sperimentali, sono sempre rimasti scettici nei confronti di una teoria che non permetteva loro di fare alcunché: non c’era nessuna previsione da verificare, nessun dato da misurare.
Non sono un fanatico delle stringhe, né sono certo che siano la chiave con cui apriremo i misteri dell’universo, ma penso comunque che queste critiche siano ingenerose. All’accusato, cioè a chi propugna una teoria, si chiede di provare la sua innocenza, mentre dovrebbero essere gli accusatori, cioè gli scettici, a provare che è colpevole. Sono necessari molto tempo e molta fatica per concepire idee così radicalmente nuove, inoltre la teoria delle stringhe è tecnicamente molto complicata. In linea di principio è in grado di fare previsioni verificabili, il problema è che i calcoli relativi sono straordinariamente lunghi e difficili. Una quarantina di anni fa
anche la teoria quantistica dei campi attirava le stesse critiche; ebbene, alla fine i conti sono stati fatti, grazie a nuove tecniche matematiche e nuovi computer più potenti, le prove di laboratorio eseguite e oggi non c’è altro settore della scienza dove si trovi un accordo più perfetto tra teorie ed esperimenti…”

Nota 2

Perché nelle teorie di stringa è molto importante il numero 8?
a) è strettamente collegato agli ottonioni, numeri complessi connessi alla somma di 8 quadrati, così come i quaternioni sono connessi alla somma di quattro quadrati e i numeri complessi alla somma di due quadrati.
b) è connesso anche ai “Numeri di Grassmann” (vedi omonima voce di Wikipedia), importanti nella fisica quantistica e nel modello standard: essi formano uno spazio di Hilbert connesso ad n fermioni 2^3=8 – dimensionale se n=3;
c) 8 è anche un numero di Fibonacci, connesso a 2 x 8=16=26 – 10 dimensioni (con 26/2 = 13 e 10/2 = 5 e 5, 8 e 13 sono tutti e tre numeri di Fibonacci;
d) è connesso infine al gruppo di Lie E8 x E8.

Dall’articolo di Pergiorgio Odifreddi “Il gruppo delle stringhe” (Rif. 6)
“…Che cos’è, però, E8? Con questo stesso nome si indicano oggetti diversi, benchè tutti collegati tra loro e, ovviamente, con il numero 8. Uno di questi oggetti è l’insieme dei vettori ad otto componenti reali la cui lunghezza al quadrato…
Prendendo tutte le combinazioni lineari di questi vettori si ottiene il reticolo di radici E8 a 8 dimensioni: E combinando questi due oggetti in un sistema di coordinate a 240 + 8=248 dimensioni si ottiene l’algebra di Lie E8, che dotata di un’opportuna struttura differenziale diventa il gruppo di Lie E8…”.

Infine segnaliamo questo recente lavoro (di Francesco Di Noto, Michele Nardelli, Pierfrancesco Roggero), dove proponiamo la nostra sezione semiaurea, basata sui numeri di Fibonacci e loro medie aritmetiche spesso semi-intere. La sezione semiaurea emerge nei numeri quantici degli orbitali elettronici dei superatomi attualmente in fase di sperimentazione, ma anche nell’andamento degli enormi numeri primi di Mersenne, e altrove. Infine un accenno ai doppi di Fibonacci, o sezione doppio aurea o per brevità “duplicaurea”, anche questa coinvolta nella fisica, in questo caso nelle stringhe, in particolare nei numeri di dimensioni coinvolte, e nel calcolo delle probabilità.

Francesco Di Noto, Michele Nardelli

(Articolo originale: NarDiNot4.pdf)

Riferimenti:

1.) “Proposta di dimostrazione della variante di Lagarias (equivalente all’Ipotesi di Riemann RH, con RH1 = RH)”

2.) “L’equivalenza di Lagarias RH1 = RH esaminata solo
con i numeri fattoriali”

3.) Articoli vari del Dott. Michele Nardelli nel suo sito http://xoomer.virgilio.it/stringtheory
4.) Link degli articoli sul database Solar del CNR “Solar – EPrints immessi da Michele Nardelli”
5.) Voce “I numeri di Grassmann” su Wikipedia
6.) Articolo “Il gruppo delle stringhe” di Piergiorgio Odifreddi sulla rivista “Le Scienze” maggio 2007
7.) “An exceptional Simple Theory of Everithing” di A.Garrett Lisi