1.Introduzione
Nel 1997 e 1999, almeno 9 formazioni si collegavano strettamente alla nuova forma scoperta dell’Universo. Se questo servisse per portare la nostra attenzione a questa notizia poco pubblicizzata o sia dovuto al fatto che queste forme geometriche (ottaedro e tetraedro) si trovano in molti ambienti e livelli della natura o per altre ragioni, non saprei dire con certezza.
2. Superclusters di galassie nell’ottaedro di Battaner

foto dal libro di Kasahara e Takahama
Grazie al telescopio orbitante Hubble e ad altri nuovi telescopi esterni all’atmosfera terrestre che hanno scattato immagini più dettagliate e chiare di quelle da terra, è stato possibile dal 2000, creare nuove mappe del cielo, con galassie, gruppi di galassie e super-clusters di galassie. Tramite le onde radio, i raggi-x e altre misurazioni, sono state localizzate molte galassie non visibili.
Questi dati sono stati combinati ed è risultato che i super-clusters conosciuti si raccolgono lungo linee e punti di intersezione che formano almeno 4 ottaedri locali, che sono uniti per i vertici in una specie di schema cristallino. Tra questi ottaedri e al loro interno, ci sono vuoti relativi di campi magnetici e galassie e dovrebbero contenere molta materia oscura. Questa è la più grande struttura nell’Universo direttamente osservata.
Questo suggerisce che l’energia, influenzata ed organizzata dai campi magnetici nel lontano passato della storia dell’universo, come anche predetto dalla teoria delle superstringhe, si è distribuita lungo filamenti e combinata in luminosi gruppi di oggetti astronomici, come l’acqua che cade su una ragnatela. La materia oscura è collassata e sotto pressione è divenuta luminosa. Oltre a questo, le mappe dello sfondo di radiazione cosmica (CMB), sembrano mostrare una forma sferica che contiene superclusters di galassie in un disco piatto, come una galassia gigante.
Le prossime illustrazioni in questa sezione, vengono dagli articoli sulla forma dell’Universo.
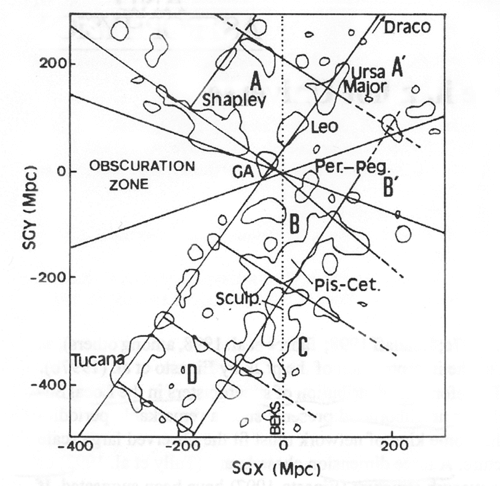
Vediamo due vicini ottaedri, visti dalla posizione del nostro sole vicina al loro punto di contatto. I super-clusters, che possono contenere miliardi di galassie, si trovano lungo i bordi e agli angoli delle forme e i vuoti relativi si trovano nelle forme. Dato che una estremità dell’area Piscis-Cetus punta all’esterno, potrebbe essere spinta da una forma in scala ancora superiore.
Giudicando dalla sua insignificante posizione nella nostra galassia, la Via Lattea, il nostro sole difficilmente può essere un principale centro nell’Universo, quindi dalla mappa mi chiedo se si vedrebbero ottaedri da entrambi i lati, da qualsiasi posizione nello spazio.
Ecco una mappa piatta dei quattro ottaedri (con una parte di altri due) che possiamo davvero osservare nei cieli, perchè si trovano nell’area di spazio più vicina a noi.
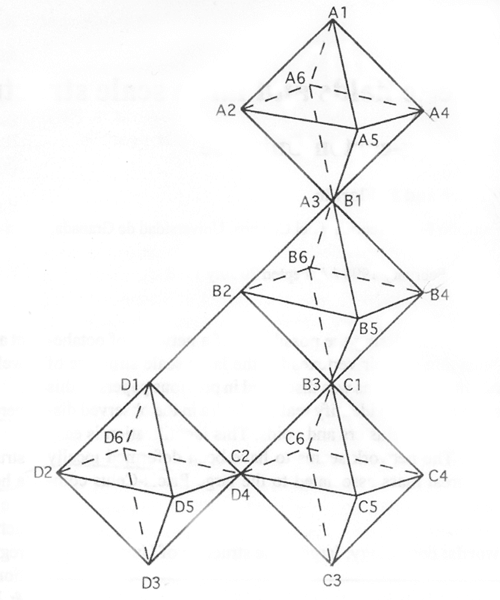
Vediamo la stessa area in ottaedri tridimensionali. “A” e “B” sono queste forme vicine a noi, mentre “C” e “D” sono più lontane e quindi meno osservabili e misurabili.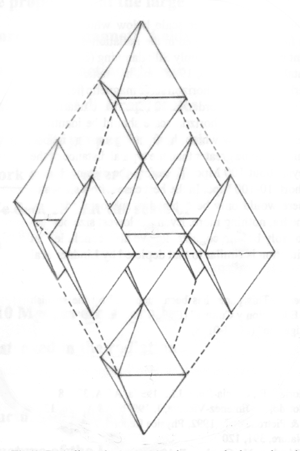
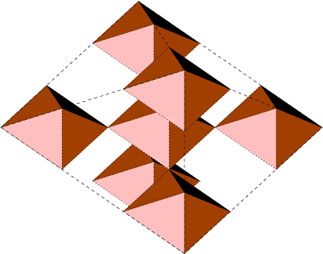
Ogni ottaedro può contenere altri ottaedri, come in un frattale. Le rappresentazioni di sopra mostrano la possibilità più semplice: 7 sub-ottaedri della dimensione di 1/3 di quello più grande. La forma più semplice seguente, sarebbero 25 sub-ottaedri della dimensione di 1/5 di quello più grande. Secondo la teoria principale al momento, le forme osservate possono avere solo una scala inferiore e diretta o iterazione, prima che le forze storiche di radiazione neghino il magnetismo necessario, strappando i filamenti. Comunque potrebbero essere innumerevoli le iterazioni nello spazio, ottaedri in ottaedri più grandi, ecc..
Secondo la teoria “cartone delle uova“, possono esistere anche innumerevoli ottaedri adiacenti.
3. Esempi 3-D a livello del sistema solare
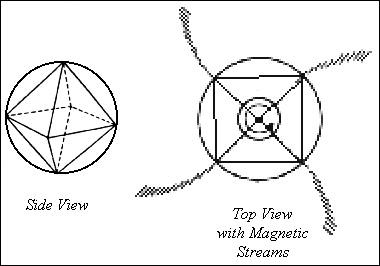
Anche il nostro sole possiede un sistema magnetico ottaedrico: polo nord, polo sud e 4 poli lungo l’equatore. In questi punti il sole emetti flussi di particelle cariche.
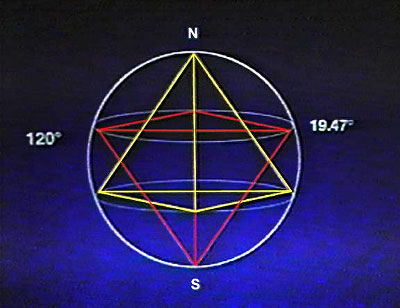
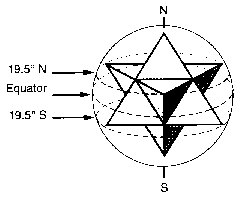
Se mettiamo un tetraedro a stella in un pianeta sferico, i punti di intersezione o “punti di stress” a 19.47° di latitudine, si mostreranno dove troviamo forti rilasci di energia e interazione tra l’interno e l’atmosfera del pianeta. Evidentemente, le continue vibrazioni planetarie creano pressione inferiore e le pressioni superiori sfuggono. Come esempi abbiamo la Grande Macchia Rossa di Giove, il Grande Punto Oscuro di Nettuno, l’area vulcanica delle Hawaii sulla Terra, le più grandi “macchie solari” nel sole.

Il sole stesso (vicino alla freccia direzionale) si muove a spirale lungo il suo braccio galattico della Via Lattea. Le quattro orbite a spirale attorno al sole, sono quelle dei suoi 4 pianeti più vicini: Mercurio, Venere, Terra e Marte.

Queste sono le proporzioni della distanza orbitale media di Mercurio dal Sole, a Venere. Nel disegno sotto, l’orbita di Mercurio toccherà i tre centri dei cerchi adiacenti e Venere sarà sulle tangenti di quei cerchi.
4. Solidi Platonici

Tutti i solidi Platonici entrano perfettamente nella sfera e molti di essi possono entrare precisamente in versioni più grandi di altri.
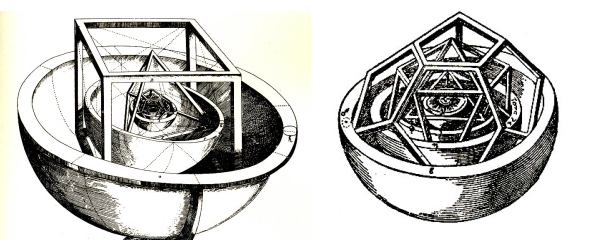
Keplero ha ipotizzato che le distanze orbitali dei 6 pianeti più vicini al Sole, potevano contenere le forme dei cinque solidi Platonici. Le variazioni orbitali ellittiche dei pianeti sarebbero contenute nei gusci sferici che li separano.
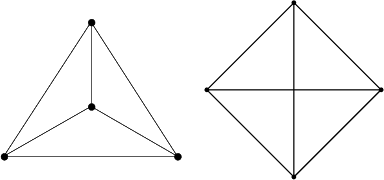
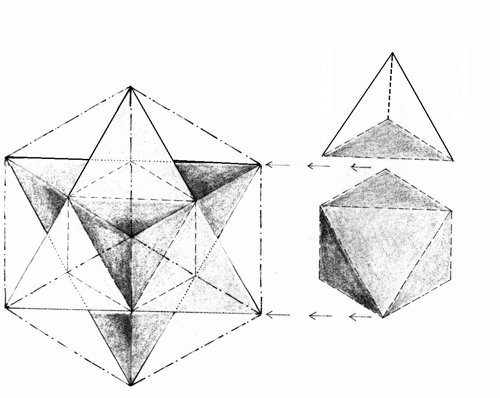
Ottaedro
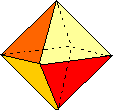

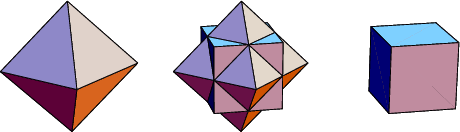
Un ottaedro è un solido simmetrico con 8 triangoli equilateri come superficie, una specie di piramide con 4 facce, sopra un’altra piramide a quattro facce invertita.
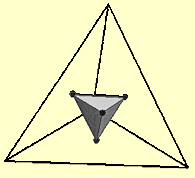
Tetraedro

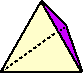
Un tetraedro è un solido simmetrico con 4 triangoli equilateri in superficie, come una piramide con 3 facce e una base. Si tratta della forma simmetrica tridimensionale più semplice fatta con linee rette, come lo è il triangolo in due dimensioni.
I diagrammi di sopra mostrano tre viste di un tetraedro, il primo, con la linea tratteggiata, è da una prospettiva laterale, il secondo dipende da come scegliete il punto centrale. La terza vista è attraverso due lati trasparenti, notate che può essere un ottaedro visto da sopra!
Il tetraedro è l’unico poligono regolare (forma 3-D con lati e angoli uguali) che si ripete direttamente su piani più piccoli. Connettendo i punti mediano dei suoi lati, troviamo tetraedri più piccoli…

Visto da un lato, il tetraedro sembra un triangolo equilatero, che implica quattro triangoli equilateri più piccoli.
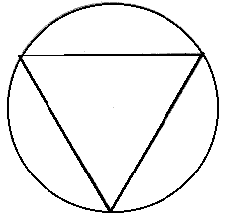
Un triangolo equilatero dentro un cerchio o un tetraedro dentro una sfera, visto da sopra

Lo stesso tetraedro dentro la stessa sfera, ma visto di lato, ci mostra questo triangolo dentro il cerchio. I suoi angoli superiori sono i 19.5° sull'”equatore” descritti in precedenza. I rapporti in queste illustrazioni si trovano spesso nei cropcircles che contengono triangoli.
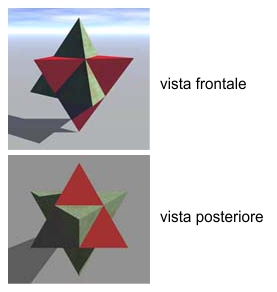
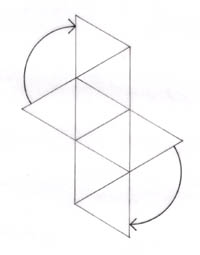
Due tetraedri possono sovrapporsi e formare un “tetraedro a stella”, che in due dimensioni è la “Stella di Davide” o “Sigillo di Salomone” (padre di Davide), conosciuta per i suoi significati esoterici. Lo possiamo vedere fermo o in movimento, oppure con un tetraedro che ruota inversamente rispetto all’altro, o in modo perpendicolare, dove il verde gira orizzontalmente e il rosso verticalmente.
Come capisco dal riferimento di Jens Rowald al lavoro di Richard Hoagland e Stan Tenet, sulla fisica tetraedrica, il percorso di energia dal centro di una sfera rotante alla sua superficie, prenderà una forma a spirale creando un tetraedro che tocca tale superfce. Il tetraedro perpendicolare creerà l’energia a spirale e le linee elettromagnetiche dove punti di energia si raccolgono in materia. I tetraedri rotanti di dimensione differente si intrecceranno.
L’energia da piani rotanti e più forti, si muoverà verso l’interno attraverso la nostra atmosfera (creando la forma di una piramide rotante invertita), finchè non si concentra in un punto e quindi torna ad uscire (come una piramide controrotante) verso e attraverso la terra. Per questo le piramidi Egizie potrebbero rappresentare la concentrazione di energia tra la Terra e lo Spazio.
Allo stesso modo della struttura di distribuzione delle foglie o dei rami di un albero rispetto al suo sistema di radici, che connette l’atmosfera con la profondità della terra. L’energia fresca entra nel sistema vivente planetario e quella saturata ne esce. Anche l’acqua si muove tra spirali più grandi e più piccole.
5. Il frattale tetraedrico di Chilbolton


Questa formazione o disposizione di componenti è stata usata nella tecnologia dei telefoni cellulari.

Estendendo il frattale, abbiamo questo triangolo composto da triangoli più piccoli o visto da sopra, una piramide fatta di livelli progressivi di piramidi più piccole.

Come vedremo presto, i triangoli rossi rappresentano anche una visione laterale di ottaedri 3d più piccoli incorporati in un tetraedro.
Come altrimenti si relazionano direttamente ottaedri e tetraedri? Se mettete due ottaedri a fianco con un lato in comune, lo spazio tra loro sarà occupato da un tetraedro. Quindi, se prendete un grosso ottaedro e lo riempite con ottaedri più piccoli con i bordi che si toccano, tutti gli spazi tra loro saranno riempiti da tetraedri.
6. Ottaedro 3-D di Overton

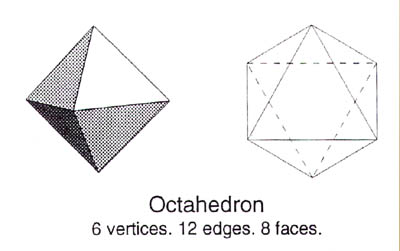
La difficoltà nel mostrare solidi girevoli nelle formazioni dei cropcircles, sta nel rappresentare 4 o più dimensioni in 2 dimensioni. Mettendo da parte gli esagoni più piccoli e trattando i più grandi come punti su linee, otteniamo un ottaedro 3D. Notate che la vista 2D di un ottaedro a sinistra ci da un quadrato e a destra un esagono.
Aggiungendo un tetraedro più piccolo ad ogni lato dell’ottaedro, abbiamo un tetraedro a stella.
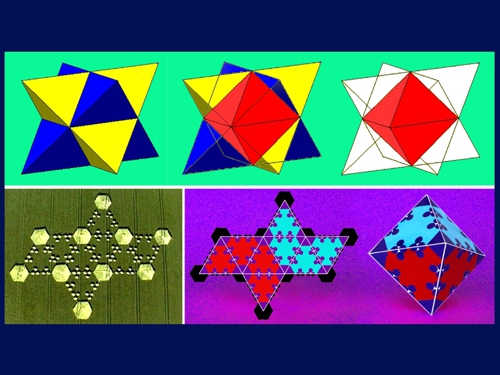
Ora vediamo come il cropcircle in basso a sinistra, quando piegato nell’ottaedro, incorpora gli esagoni più grandi e piccoli, rinforzando gli schemi lungo i suoi bordi e vertici. Vedete come un ottaedro rientra nell’area di intersezione di un tetraedro a stella. Forse in una certa scala, l’enorme ottaedro universale si rivelerà dentro un tale tetraedro a stella o altro solido Platonico?
7. Frattali di Windmill Hill e West Kennett

Prima, in luglio, i due schemi bidimensionali, fatti di piante erette e altre sdraiate.

Quindi questa formazione in agosto, ora fatta con piante sdraiate su uno sfondo eretto, abbassando intelligentemente le piante in due direzioni avremo questo risultato da ogni punto di vista aereo.
Le ombre evidenziano questo schema tridimensionale: la metà superiore di un ottaedro, con le sue iterazioni frattali inferiori e i cerchi esterni che possono implicare “e così di seguito”. Notate che le diagonali non sono fatte di semplici linee rette, ma di una serie di “scalini” alternati.
Ecco i contorni del cropcircle
Questo è un modo per illustrare la relativa dimensione ed altezza delle piramidi. Nello schema del cropcircle, chiaramente, le piramidi si sovrappongono.
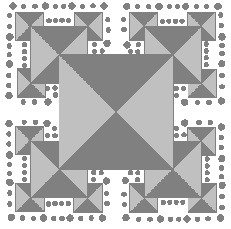
Ecco la disposizione del frattale, contiene complessi di piramidi, semplificati ed evidenziati con l’ombreggiatura.
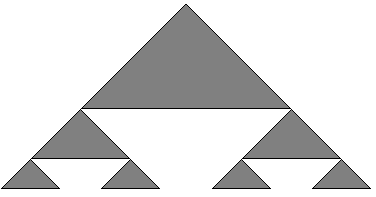
Questa sarebbe una sezione orizzontale del precedente disegno, da lato a lato, ignorando la dimensione fronte e retro. Abbiamo una forma simile a quella precedente di Sierpinski.
8. Tetraedro di Winterbourne Basset


Specificando la direzione del grano, Martin evidenzia altri livelli di forma triangolare impliciti.
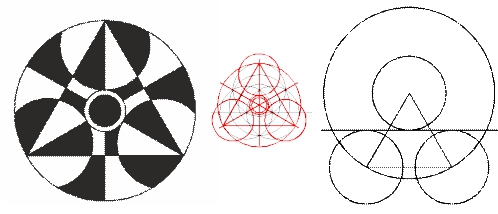
Questo mostra il lavoro dell’astronomo Gerald Hawkins sui cropcircles:
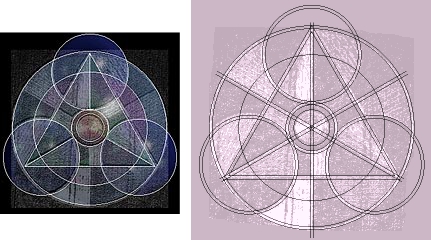
La proporzione tra il diametro del cerchio qua mancante, che tocca gli angoli del triangolo equilatero, rispetto al diametro dei cerchi più piccoli, è 4:3. Inoltre, una tangente ad ognuno dei due cerchi più piccoli, toccherà anche il terzo cerchio.

Questo è un esempio del teorema numero due di Hawkins, in questo schema, spesso implicito nei simboli dei cropcircles, l’area dei cerchi circoscritti e inscritti è 4:1.
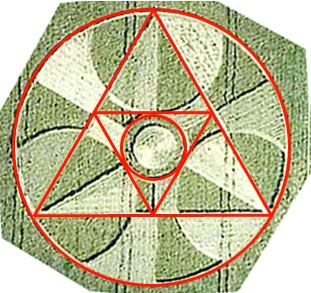
Hawkins sottolinea che col teorema due, il cerchio circoscritto (esterno) è 4 volte più grande del cerchio interno qui mancante, che tocca i lati del triangolo più grande. Inoltre questa proporzione si ripete per un triangolo attorno al più grande dei cerchi interni. Questo ci da un rapporto tra l’area del cerchio più grande e quella del cerchio interno più grande, di 8:1, che corrisponde alla nota musicale “DO”.
9. Estensioni 3-D
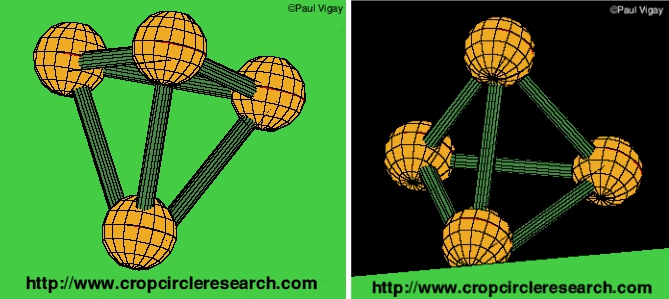
Le figure di Paul non erano tratte dal cropcircle di Winterbourne Basset. Completando e gonfiando le sfere di questo cropcircle e ingrossando le loro linee di connessione, allargando poi l’intera figura, abbiamo la variazione 3D numero uno.
Qui Martin Keitel completa i cerchi di dimensione media e aggiunge un cerchio logico che unisce i loro centri. La versione di destra risponde al disegno reale del cropcircle.
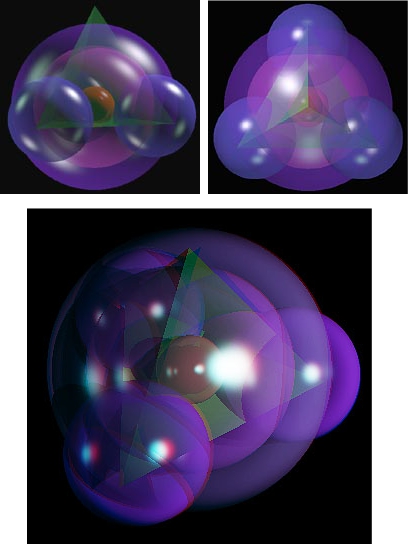
“Gonfiando” tutto abbiamo la variazione 3D numero due.
Un modo in cui si può muovere: la sfera centrale ruota in senso anti-orario rapidamente, il tetraedro gira meno rapidamente in senso orario, le sfere agli angoli ruotano perpendicolarmente in senso anti-orario a velocità media, la sfera nel centro ruota perpendicolarmente ma in senso orario a velocità inferiore, la sfera esterna ruota verso nord-ovest lentamente.
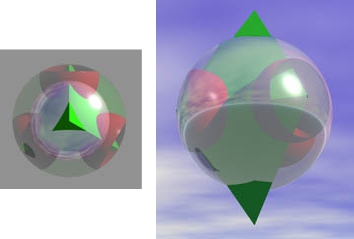
Aggiungendo la sfera nel mezzo e un tetraedro logico che punta dall’altra parte dietro al primo abbiamo la variazione 3D numero tre.
10. Formazione Sierpinski di Hackpen Hill


Questo crop-circle mostra altro tipo di formazione Sierpinski che si espande all’esterno, invece che verso l’interno
11. Frattali Koch di Silbury e Milk Hill

Ora, una estensione della formazione di Hackpen Hill nel frattale a stella di Koch

Quindi un mese dopo…lo stesso frattale di Koch con questa forma interna a “fiocco di neve”, perchè anche se a prima vista la forma interna sembra così diversa dal frattale a stella esterno, il fiocco di neve è creato dagli stessi elementi della stella esterna.
Tutte le rientranze sono fatte di mezze stelle o punti-stella che si rivolgono all’interno, invece che nella stella esterna. Le proiezioni a “singolo-dito” che puntano all’esterno, sono miniature delle proiezioni della stella esterna che puntano verso l’interno. I cerchi dentro il fiocco di neve sono fuori dalla stella.
Tre iterazioni del frattale di Koch. Il cropcircle contiene il secondo esempio, ma il secondo è suggerito dai cerchi circostanti in due grandezze.

Vediamo altre ingegnose correlazioni tra le forme interne ed esterne.
12. Il mistero della forma piramidale di Silbury

Grazie alla sua disposizione meravigliosa, da qualsiasi angolo venga fotografata, l’ombreggiatura darà un effetto 3d affascinante.
Questa foto di Lucy Pringle è una delle più belle che conosco. Ancora, la struttura organica viene accentuata dalle “diagonali” fatte come “scalini irregolari” invece che rettilinee. Vedete come è stato posizionato il grano “attorno agli angoli”, come un tappeto sulla scala che fluisce nel piano più largo, che a sua volta porta nelle scale seguenti mentre la formazione ruota.
Altre informazioni suggerite:
1. “Crop Circle Geometry – 3-D Forms”
2. “Crop Circle Geometry – size, placing and ratios”
3. “Crop Circle Geometry – 3 D crop circle models”
4. “The perfect circular geometry of the Harlequin Triangle”
5. “The next dimension of the Harlequin Triangle”
6. “Gerald Hawkins’ Latest Work, Part 4”
7. “Interesting Shapes & 3D Geometry”
8. “Dr Gerald Hawkins’ Elusive Fifth Theorem!”
9. “Crop Circles – The Hidden Form“
Solidi Platonici
1. “Octahedron”
2. “Tetrahedron”
3. “Regular Polyhedra or Platonic Solids“
La forma dell’Universo locale
1. “The ‘Matrix’ is a Reality”
2. “The fractal octahedron network of the large scale structure”
3. “Large scale structure and magnetic fields”
4. “A tentative history of cosmological magnetic fields”
5. “Magnetic fields and large scale structure in a hot Universe, IV. The egg-carton Universe”
6. “When the Universe was ‘spongy’”
7. A little book of Coincidence, by John Martineau, Wooden Books, 2001.
Tradotto da Richard per Altrogiornale.org
© Jonah Ohayv (4/2004)
korncirkler.dk