
Nel XIX secolo, la scoperta dei quaternioni da parte del matematico irlandese William Hamilton fornì uno strumento per descrivere le rotazioni nello spazio, cambiando per sempre la fisica e la matematica.
Immaginiamo di spostare indietro la lancetta delle ore di un orologio dalle tre a mezzogiorno. Da tempo i matematici sanno descrivere questa rotazione come una semplice moltiplicazione: un numero che rappresenta la posizione iniziale della lancetta delle ore sul piano viene moltiplicato per un altro numero costante. Ma esiste un trucco per descrivere le rotazioni nello spazio? Il buon senso dice sì, ma William Hamilton, uno dei matematici più prolifici del XIX secolo, cercò per oltre un decennio di trovare la matematica per descrivere le rotazioni in tre dimensioni. L’improbabile soluzione lo portò al terzo dei soli quattro sistemi numerici che sono in stretta analogia con l’aritmetica standard, contribuendo a stimolare l’ascesa dell’algebra moderna.
I numeri reali formano il primo di questi sistemi numerici. Formati da una sequenza di numeri che possono essere ordinati dal più piccolo al più grande, i numeri reali includono tutti i personaggi familiari che impariamo a conoscere a scuola, come -3,7, la radice quadrata di 5, e 42. Gli algebristi del Rinascimento incapparono nel secondo sistema di numeri che possono essere addizionati, sottratti, moltiplicati e divisi quando si resero conto che risolvere determinate equazioni richiedeva un nuovo numero, i, che non si trovava in alcun luogo sulla retta dei numeri reali. Fecero i primi passi al di fuori di quella retta e nel “piano complesso”, dove numeri ingannevolmente chiamati “immaginari” si accoppiano con numeri reali così come le lettere maiuscole si accoppiano con numeri nel gioco della Battaglia navale. In questo mondo planare, i “numeri complessi” rappresentano frecce che è possibile far scorrere avanti e indietro con addizione e sottrazione o far ruotare e allungare con moltiplicazione e divisione.
Hamilton, il matematico irlandese che diede il nome all’operatore
“Hamiltoniano” nella meccanica classica e quantistica, sperava di uscire dal piano complesso aggiungendo un asse immaginario j. È un po’ come se Milton Bradley, azienda produttrice statunitense di giochi, avesse trasformato “Battaglia navale” in “Battaglia sottomarina” con una colonna di lettere minuscole. Ma c’era qualcosa nelle tre dimensioni che rovinava ogni sistema a cui Hamilton potesse pensare. “Deve aver provato milioni di cose ma nessuna di esse funzionava”, ha detto John Baez, matematico dell’Università della California a Riverside. Il problema era la moltiplicazione. Nel piano complesso, la moltiplicazione produce rotazioni. Qualunque fosse la definizione della moltiplicazione in tre dimensioni, Hamilton non riusciva a trovare una divisione, operazione opposta alla moltiplicazione, che desse sempre risposte significative.
Per capire che cosa rende la rotazione tridimensionale molto più difficile, basta paragonare la rotazione del volante di un’auto alla rotazione di una mappamondo. Tutti i punti sul volante si muovono insieme allo stesso modo, quindi sono moltiplicati per lo stesso numero (complesso). Invece punti sul mappamondo si muovono più velocemente intorno all’equatore e più lentamente se ci si sposta verso nord o verso sud. Ed è cruciale osservare che i poli non cambiano affatto. Se le rotazioni in 3-D funzionassero come le rotazioni 2-D, ha spiegato Baez, ogni punto si muoverebbe.
La soluzione, che uno scellerato Hamilton incise, secondo un aneddoto famoso, sul Broome Bridge di Dublino quando finalmente la trovò il 16 ottobre 1843, fu quella di fissare il globo in uno spazio più ampio, dove le rotazioni si comportano in modo più simile a come fanno in due dimensioni. Con non due ma tre assi immaginari, i, j e k, più la linea dei numeri reali a, Hamilton poté definire nuovi numeri che sono come frecce nello spazio 4-D. Li chiamò “quaternioni”. All’imbrunire, Hamilton aveva già delineato uno schema per la rotazione delle frecce 3-D: dimostrò che queste potevano essere pensate come quaternioni semplificati, creati ponendo a, la parte reale, uguale a zero e mantenendo solo i componenti immaginari i, j e k, un terzetto per il quale Hamilton inventò il termine “vettore”. Ruotare un vettore tridimensionale significava moltiplicarlo per una coppia di quaternioni 4-D completi contenenti informazioni sulla direzione e il grado di rotazione. (Per la moltiplicazione con i quaternioni in azione, si veda questo video.)
Tutto quello che si potrebbe fare con i numeri reali e complessi, si potrebbe fare anche con i quaternioni, tranne che per una differenza irritante. Mentre le moltiplicazioni 2 × 3 e 3 × 2 danno entrambe 6 come risultato, l’ordine è importante per la moltiplicazione dei quaternioni. I matematici non avevano mai visto prima questo comportamento nei numeri, anche se riflette il modo in cui ruotano gli oggetti di tutti i giorni. Per esempio, posizioniamo uno smartphone rivolto verso l’alto su una superficie piana. Facciamolo ruotare nel piano di 90 gradi verso sinistra, e poi voltiamolo. Notiamo la posizione della fotocamera. Ripartiamo dalla posizione originale: ora prima lo voltiamo col display a faccia in giù e poi lo facciamo ruotare sul piano di appoggio verso sinistra. La posizione della fotocamera è cambiata. Questa proprietà inizialmente allarmante, nota come non commutatività, è una caratteristica che i quaternioni condividono con la realtà.
Ma anche nel nuovo sistema numerico si nascondeva un baco. Se uno smartphone o una freccia ruotano di 360 gradi, il quaternione che descrive questa rotazione a 360 gradi ruota solo di 180 gradi nello spazio quadridimensionale. Sono necessarie due rotazioni complete dello smartphone o della freccia per riportare il quaternione associato al suo stato iniziale. (Fermarsi dopo una rotazione lascia il quaternione invertito, poiché i numeri immaginari elevati al quadrato sono pari a -1.)
Le frecce capovolte producono segni negativi spuri che possono essere devastanti in fisica, quindi quasi 40 anni dopo il vandalismo di Hamilton sul ponte, i fisici entrarono in guerra l’uno con l’altro per impedire al sistema dei quaternioni di diventare uno standard. Le ostilità scoppiarono quando un professore di Yale di nome Josiah Gibbs definì il vettore moderno. Decidendo che la quarta dimensione era decisamente troppo disturbante, Gibbs decapitò la creazione di Hamilton omettendo completamente un termine; per questo derivato dai quaternioni, Gibbs mantenne la notazione i, j, k, ma divise l’ingombrante regola per moltiplicare i quaternioni in operazioni separate per moltiplicare i vettori che ogni studente universitario di matematica e fisica impara oggi: il prodotto scalare e il prodotto vettoriale. I discepoli di Hamilton etichettarono il nuovo sistema come un “mostro”, mentre i fan del vettore denigrarono i quaternioni come “vessatori” e un “puro male”. Il dibattito infuriò per anni nelle pagine di riviste e opuscoli, ma la facilità d’uso alla fine portò i vettori alla vittoria.
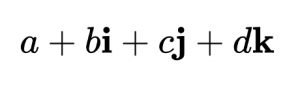
I quaternioni languirono all’ombra dei vettori fino a quando la meccanica quantistica rivelò la loro vera identità negli anni venti. Mentre i normali 360 gradi sono sufficienti per ruotare completamente i fotoni e le altre particelle che mediano le forze, agli elettroni e a tutte le altre particelle di materia occorrono due giri per ritornare allo stato iniziale. Il sistema numerico di Hamilton descriveva queste entità non ancora scoperte, ora note come “spinori”, fin dall’inizio.
Tuttavia, i fisici non hanno mai adottato i quaternioni nei loro calcoli quotidiani, perché è stato trovato uno schema alternativo per la gestione degli spinori basato sulle matrici. Solo negli ultimi decenni i quaternioni hanno vissuto una rinascita. Oltre a essere stati adottati nella grafica al computer, dove servono come strumenti efficienti per il calcolo delle rotazioni, i quaternioni vivono nella geometria delle superfici a dimensioni più elevate. Una superficie, in particolare, chiamata varietà iperkähler, ha la caratteristica intrigante di permettere di passare agevolmente da gruppi di vettori a gruppi di spinori e viceversa, conciliando i due fronti della guerra dell’algebra vettoriale. Poiché i vettori descrivono le particelle di forza mentre gli spinori descrivono le particelle di materia, questa proprietà è di estremo interesse per i fisici che si chiedono se esista in natura una simmetria tra materia e forze, chiamata supersimmetria. (Tuttavia, se esistesse, la simmetria dovrebbe essere gravemente violata nel nostro universo.)
Per i matematici, nel frattempo, i quaternioni non hanno mai veramente perso il loro splendore. “Non appena Hamilton inventò i quaternioni, tutti decisero di inventare il proprio sistema numerico”, ha detto Baez. “La maggior parte di essi era completamente inutile, ma alla fine… hanno portato a quello che ora consideriamo un’algebra moderna.” Oggi, gli algebristi astratti studiano una vasta gamma di sistemi numerici in qualsiasi numero di dimensioni e con ogni tipo di proprietà esotiche.

Una costruzione non così inutile si è rivelata il quarto e ultimo sistema numerico che permette una moltiplicazione analoga e una divisione associata, scoperta poco dopo i quaternioni dall’amico di Hamilton, John Graves. Alcuni fisici sospettano che questi peculiari “ottetti” a otto dimensioni possano giocare un ruolo profondo nella fisica fondamentale.
“Penso che ci sia ancora molto da scoprire sulla geometria basata sui quaternioni – ha detto Nigel Hitchin, studioso di geometria dell’Università di Oxford – ma se vuoi una nuova frontiera, allora è quella degli ottetti”.
Charlie Wood/Quanta Magazine
(L’originale di questo articolo è stato pubblicato il 6 settembre 2018 da QuantaMagazine.org, una pubblicazione editoriale indipendente online promossa dalla Fondazione Simons per migliorare la comprensione pubblica della scienza. Traduzione ed editing a cura di Le Scienze. Riproduzione autorizzata, tutti i diritti riservati)

