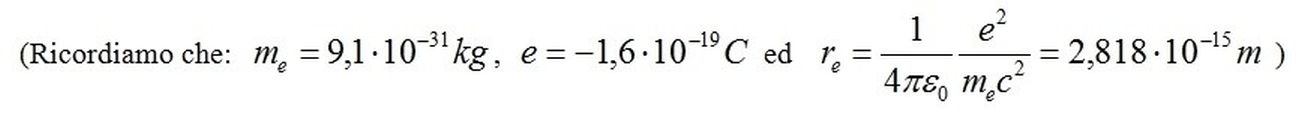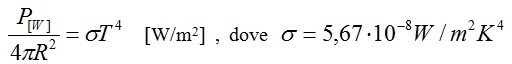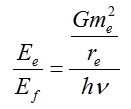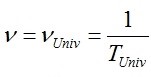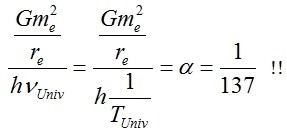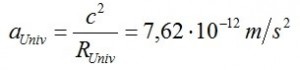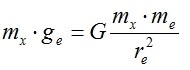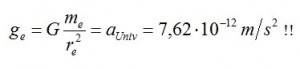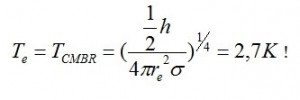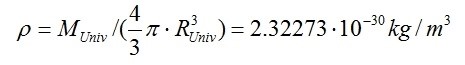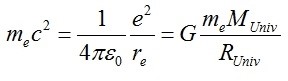Conosciamo la Legge di Hooke:
Essa ci dice che una forza esercita un’estensione od una compressione di una molla che dipende dalla costante elastica k.
Notiamo altresì che le dimensioni di k sono quelle di una forza fratto una lunghezza. Il nostro intento è quello di determinare l’universo macroscopico tramite le forze microscopiche. E notiamo altresì che le dimensioni degli atomi sono determinate dagli elettroni, che ne costituiscono il guscio; e non, dunque, dai protoni e dai nuclei.
A tal proposito, la forza elettrica per eccellenza è quella di Coulomb, ad esempio tra un elettrone ed un positrone (antielettrone) a distanza re pari al raggio classico dell’elettrone, restando in ambito elettronico:
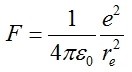
A questo punto, una costante elastica estrapolata da tale forza, per le ragioni dimensionali appena esposte, deve avere la seguente forma:
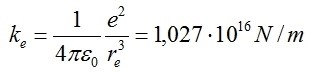
Passando al macroscopico, si immagini un elettrone che, idealmente, orbita intorno a tutto l’universo; sulla base di ciò, per Newton, possiamo scrivere la seguente forza gravitazionale:

E, anche qui, una costante elastica, per le solite ragioni dimensionali, deve avere la seguente forma:
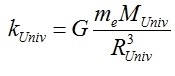
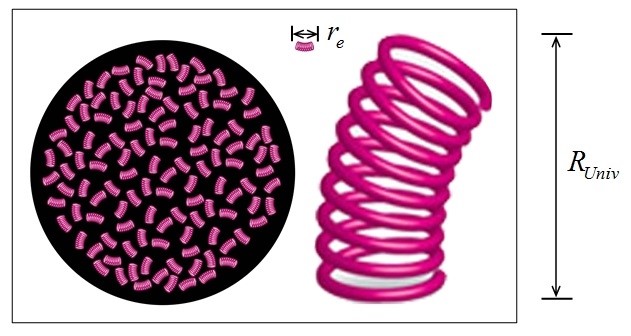
Sappiamo poi dalla fisica, banalmente, che se abbiamo N molle identiche in serie, la costante elastica complessiva è quella della singola molla divisa per N. Immaginando ora l’universo come una grossa molla composta da tante mollettine in serie (figura 1), potremo scrivere che:
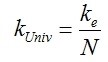
Per ultimo, osserviamo che tali mollettine in serie non sono necessariamente disposte su una retta, ma bensì in modo random, partendo da un centro, un po’ verso destra, un po’ verso sinistra, poi un po’ verso l’esterno ed un po’ verso l’interno, fino a costituire una sorta di gigante sfera che rappresenterà l’universo.
In tal caso, se le mollettine sono N e ciascuna di lunghezza re , la dimensione della macromolla complessiva non sarà N volte re , ma radice di N re , ossia:

Ciò perché, notoriamente, se consideriamo ad esempio una persona al centro di una stanza e tale persona compie N passi di un metro ciascuno ed in direzione casuale, dopo tali N passi non si troverà alla distanza di N metri dal punto di partenza, ma, notoriamente, a radice di N metri.
Va poi da sè che se ipotizzo che l’universo si compone di N mollettine elettroniche, allora sussisterà, per le masse, la seguente ovvia relazione:
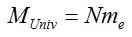
Bene, ora abbiamo tutti gli ingredienti: se nella (5) inseriamo la (2) e la (4), otteniamo:
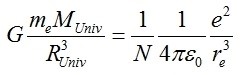
Se, ora, nella (8) inseriamo la (6) e la (7), otteniamo:
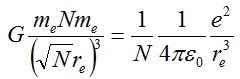
Ricavando ora N dalla (9), si ottiene:
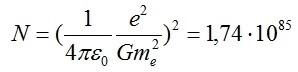
e, finalmente, ecco la carta d’identità dell’universo elastico:
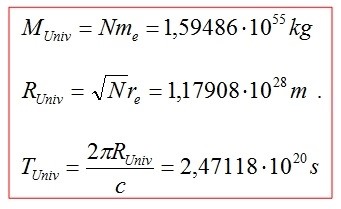
(si ha tale T poichè il periodo è dato dalla circonferenza fratto la velocità)
Per ultimo, vediamo poi che vale anche la seguente formula di unificazione:
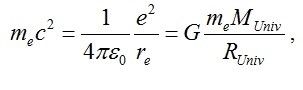
Mettiamo tutto alla prova:
1) Ricordiamo la Legge di Stefan-Boltzmann:
Ricordiamo poi la temperatura della radiazione cosmica di fondo CMBR:
Potete verificare che:
2) Voglio effettuare una comparazione (un rapporto) tra due energie: l’energia potenziale associata ad un elettrone e quella di un fotone:
ora, se la frequenza è quella ottenuta effettuando (notoriamente) il reciproco del periodo dell’universo, ossia se:
allora:
ossia proprio la Costante di Struttura Fine.
3) Mi propongo di irradiare tutta l’energia di una coppia elettrone-positrone nel tempo dell’universo; bene, la potenza corrispondente (numericamente) è esattamente pari alla costante di Planck:
4) L’accelerazione (centrifuga) è data dalla velocità al quadrato fratto il raggio; dunque, nel nostro Universo:
Mi chiedo ora se esista un “corpo celeste” la cui accelerazione di gravità sia proprio (esattamente) aUniv. Ebbene esso esiste, ed è l’elettrone! Infatti, se, in senso classico, lo immaginiamo come un piccolo pianetino, avremo che, per una massa di prova mx sulla sua “superficie”:
5) Si può dire che la TCMBR sia non solo la temperatura dell’universo, ma anche quella dell’elettrone; infatti:
6) Di passaggio, notiamo pure che vale la seguente relazione, la quale, come si può dimostrare, sancisce la sintonia tra l’universo elastico ed il Principio di Indeterminazione:
7) La densità dell’universo elastico è in accordo con quella stimata dagli astrofisici:
8) La (14) unifica la gravità e l’elettromagnetismo:
9) L’universo elastico e le curve di rotazione delle galassie (la morte della fantomatica materia oscura):
nella nostra galassia (la Via Lattea), si stima che il Sole, che evidentemente si trova ad una decina di kpc dal centro
dovrebbe avere una velocità di rotazione di 160 km/s, se la stessa fosse imputabile alla sola materia barionica della galassia stessa, ossia a quella delle stelle e di tutta la materia potenzialmente visibile (l’unica reale, a mio avviso).
Si misura, invece, una velocità di 220 km/s, ossia più grande.
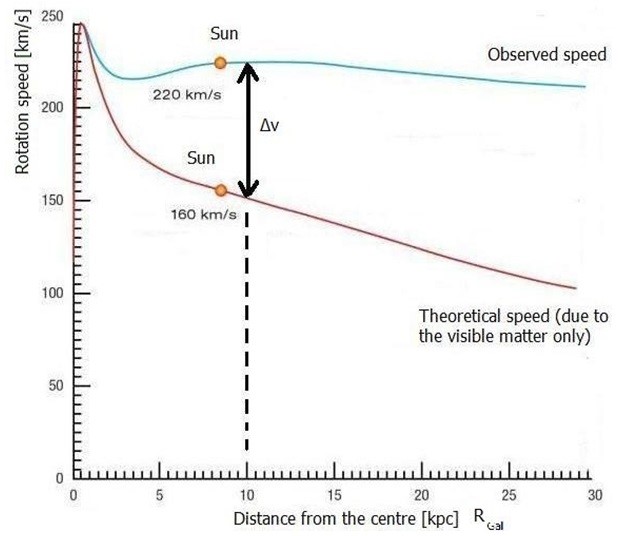
La scelta della scienza ufficiale (che, tra parentesi, è la stessa degli imbarazzanti neutrini superluminali, dell’iperfinanziato bosone divino, dell’etere cosmico, dell’energia oscura ecc) è stata quella di supporre che tale discrepanza sia dovuta all’esistenza di materia invisibile e oscura tutta intorno alle galassie; e mica poca. Spropositatamente di più di quella visibile; pensate voi. E tale materia, dicono loro, è appunto invisibile, in quanto non irradia fotoni; però, evidentemente, è trasparente, in quanto, essendo tutta intorno alla galassia, non dovrebbe permetterci di vedere la galassia stessa con i telescopi; ma noi le galassie le vediamo piuttosto bene….
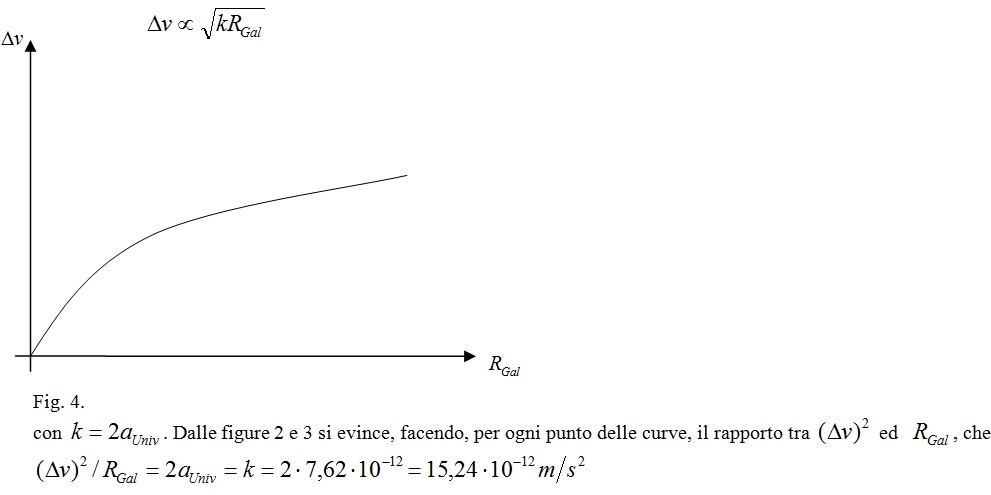
Con riferimento alla figura 2 qui sopra riportata, facciamo un attimo due conti della serva, giusto sugli ordini di grandezza. L’universo elastico è in contrazione con accelerazione:
Ora, sappiamo tutti che un oggetto che cade da un’altezza h, sottoposto all’accelerazione di gravità:
giungerà al suolo con una velocità finale vf :
Ciò ce lo insegna Newton. Bene; nel caso del Sole, l’accelerazione cosmica dell’Universo, efficace solo a grandi distanze (grandi R, in quanto tale accelerazione è piccola; da cui l’anomalia delle velocità prevalentemente alla periferia delle galassie) determina una Δv, di suo, della seguente entità:

che sono proprio quei 220-160=60km/s di Δv di discrepanza, nella figura 2 qui di sopra riportata!
E l’esattezza della formula vale su tutta la curva; ad esempio, a 25kpc, si ha un Δv=100km/s!
Ma trattasi, ripeto, di conti fatti a spanne! Come stanno di preciso le cose lo sa solo il Creatore. Non di certo i signori della fantomatica materia oscura.

Anche osservando la curva di rotazione di un’altra galassia, ad esempio della M33, qui sopra, si vede che la (15) funziona molto molto bene. Ma non è ciò che ci interessa; ciò che importa è che l’ordine di grandezza dalla forza mareale dell’Universo circostante è proprio lo stesso della forza misteriosa che imprime alle stelle una maggior velocità, nelle galassie. In ogni caso, pare che la distanza dal centro della galassia e il delta di velocità riscontrati dagli astrofisici siano uno proporzionale alla radice dell’altra; e la radice è l’operazione inversa dell’elevazione al quadrato, tipica della legge di Newton!
Grazie per l’attenzione.
Leonardo Rubino