Genesi di una curva geometrica

A cura di Gaetano Barbella
Uno scienziato nel tormento

Traggo spunto dall’articolo “Stephen Hawking era tormentato dalle domande radicali dall-esistenza di dio” di Matteo Matzuzzi, giornalista, caporedattore del giornale online Il Foglio.it.(1)

In particolare fa riferimento al relativo sottotitolo:

“La contrapposizione tra Dio e la lettura scientifica del mondo deriva da una svista filosofica“.

Tesi che l’astrofisico Marco Bersanelli, intervistato da Matteo Matzuzzi, concentra su questa domanda:

“…Ma il problema è domandarsi da dove proviene l’esserci delle cose, da dove viene questo istante, da dove viene il mio io. Questo è l’essere creati: io non mi faccio da me. Ogni cosa (se dotata di coscienza) dovrebbe domandarsi da dove proviene. La creazione – aggiunge Marco Bersanelli – non è relegata al Big bang, a quel momento in un lontanissimo passato. La creazione avviene sempre, anche ora”.

La sorte è bizzarra, e come agisce nel mistero e nell’oscurità, facendo capolino qua e là come i vaghi luminosi puntini delle stelle nel cielo notturno, così sembra rivelarsi agli occhi di uomini come Stephen Hawking tormentato dalle domande radicali, sull’esistenza di Dio. E già la stessa sorte lo aveva posto nella grave condizione di essere vincolato all’immobilità, limitato dalla patologia a comunicare con un sintetizzatore vocale. Quasi a dare una risposta, non a lui particolarmente ma al mondo della scienza che cerca di spingersi verso la stessa domanda di Hawking sulla contrapposizione dell’esistenza di Dio. Cioè a cercare al limite da matematico la formula di Dio come spingerlo in un angolino per meglio rintracciarlo.

La scienza è tanto presa per la ricerca e trascura altri generi di ricerca che potrebbero aiutarla, ma è cieca perché non trova nessi razionali per legarle. E allora, forse il segno che ci viene dall’infermità di Stephen Hawking è la demolizione del titanismo scientifico, la causa che offusca il poderosi telescopi di cui si servono gli astrofisici. Ecco il nesso trascurato. Basta così un modesto “Davide”, che con una fiondata del suo naturale minuscolo telescopio di madre natura, i suoi occhi, atterra quei titani in lui che nemmeno vede e senza essere, al limite, uno dei tanti semplici amatoriali dell’astronomia, ecco la risposta alla domanda di Marco Bersanelli dell’articolo di Matteo Matzuzzi. Ma il guaio è che anche questo scienziato è uno di loro, cioè quelli come  Stephen Hawking, incapace di credere ciò che ho detto, il segno riposto nell’infermità di Hawking, il fatidico nesso.

Un nesso che per intravederlo potrebbe cominciare da una curva geometrica intravista con un certo telescopio interiore ad un dilettante di matematica, un abile disegnatore pieno di idee ma privo di una cultura accademica. È solo un buon geometra e si sarà capito che sto parlando di me.

La curva dei poligoni regolari stellati

Non si sapeva ma occupandomi molto spesso di poligoni stellati regolari mi sono reso conto che hanno una matrice comune tramite una particolare curva che, come le spirali, curve note in geometria – per esempio la spirale logaritmica o aurea – che come regola seguono una variabile, un valore numerico che le descrivono lungo il loro ruotare rispetto a centro. Nel caso della curva di poligoni stellati regolare, di cui andremo a parlare, questo valore è espresso da:

r = 1 / cos (θ / 3)

Di seguito espongo alcuni esempi di questa curva, con grafici relativi alle figure di poligoni stellati più semplici e comuni: un ottagramma, un esagramma e un pentagramma in questo ordine.

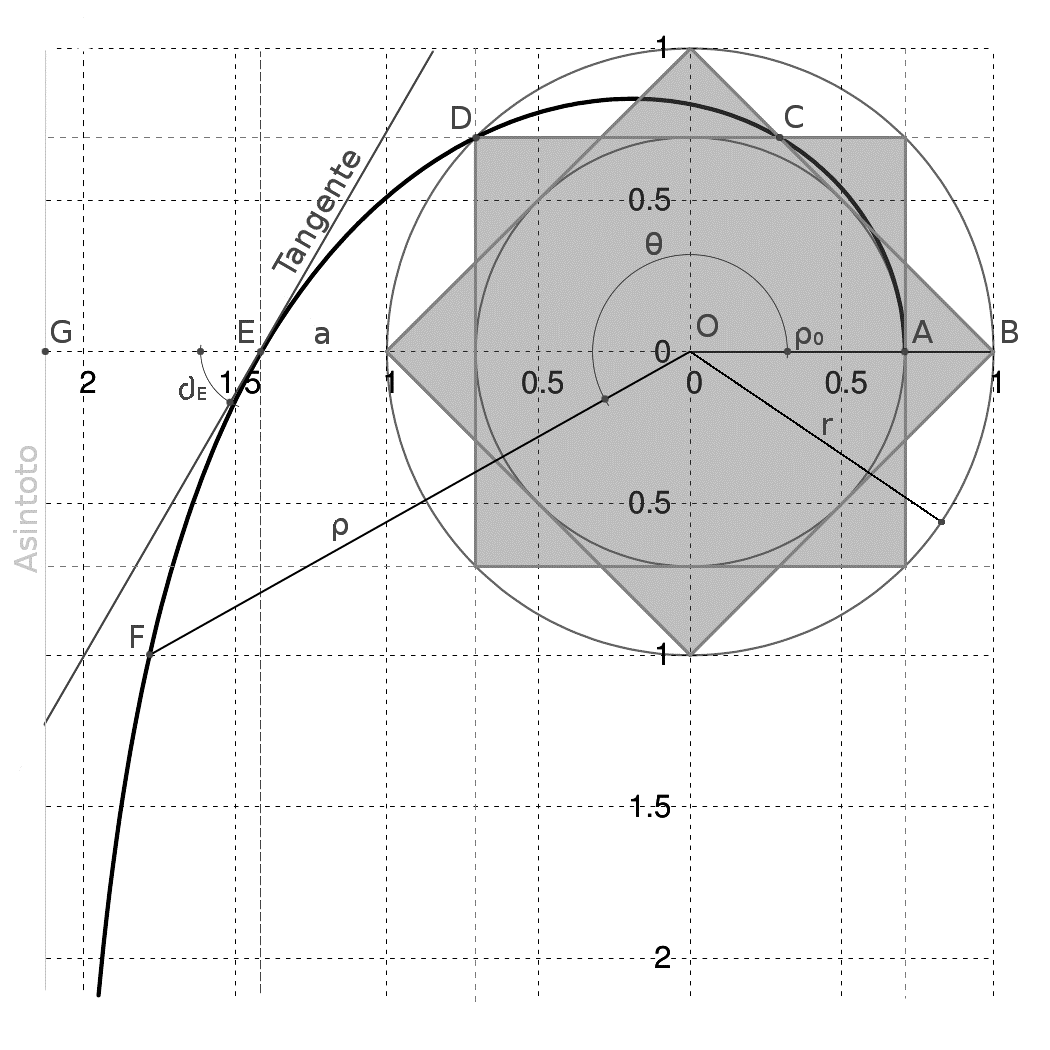
Con l’illustr. 1 figura il caso della spirale  dell’ottagramma, che si ricava così:

Si tracci il cerchio di raggio OB uguale a 1 e si costruisca l’ottagramma inscrivendovi due quadrati sfasati di un angolo retto.

Il punto A è l’inizio della curva in questione e i punti C e D individuano ulteriormente la stessa curva. Poi sull’asse orizzontale passante per il centro O si rintraccia il punto E della curva, la cui tangente è sempre di 60° rispetto l’asse orizzontale.

Infine l’asintodo della curva, che idealmente si congiunge all’infinito con la curva, segnato in verde, dista dal centro O tre volte il raggio OA.

Infine l’asintodo della curva, che idealmente si congiunge all’infinito con la curva, segnato in verde, dista dal centro O tre volte il raggio OA.

Ed ecco infine l’abaco di calcolo della curva che vale per tutti i casi di poligoni stellati, in relazione ai simboli segnati sull’illustr. 1.

Equazione polare della curva:

ρ = ρ0 / cos (θ / 3)…………………….vettore generico della curva (p. esempio nel punto F);

ρ0 = √2 ……………………………….raggio OA della circonferenza interna;

n = numero delle divisioni del poligono stellato = 360° / arccos √2 / ρ ;

δ = arctan 3 cotan (θ / 3)………  angolo di tangenza generico della curva.

a =  3 √2………………………………….distanza dell’asintoto da dal centro O.

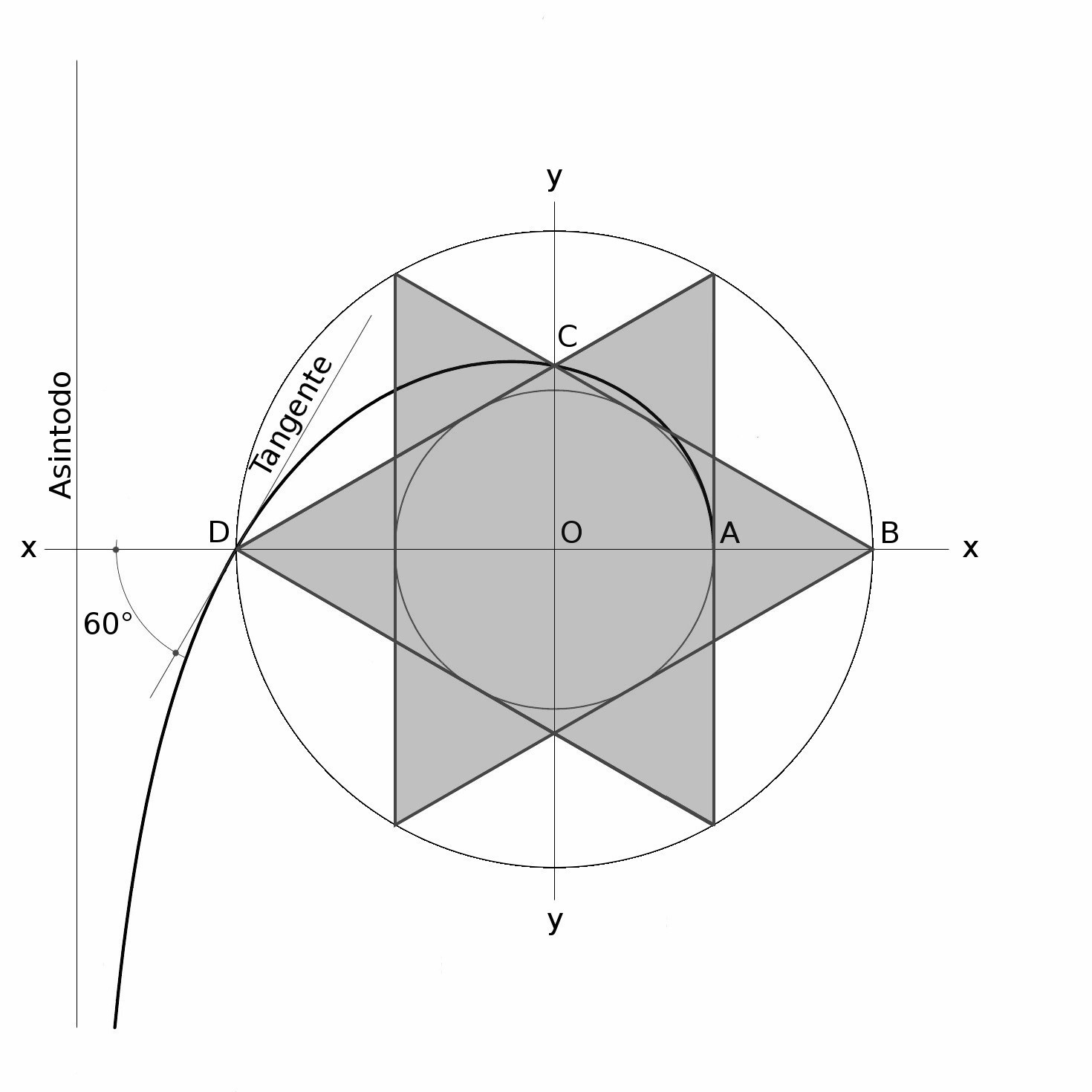
Fa seguito  il caso dell’esagramma con l’illustr. 2, i cui punti A, C e D rintracciano la curva che inizia da A.

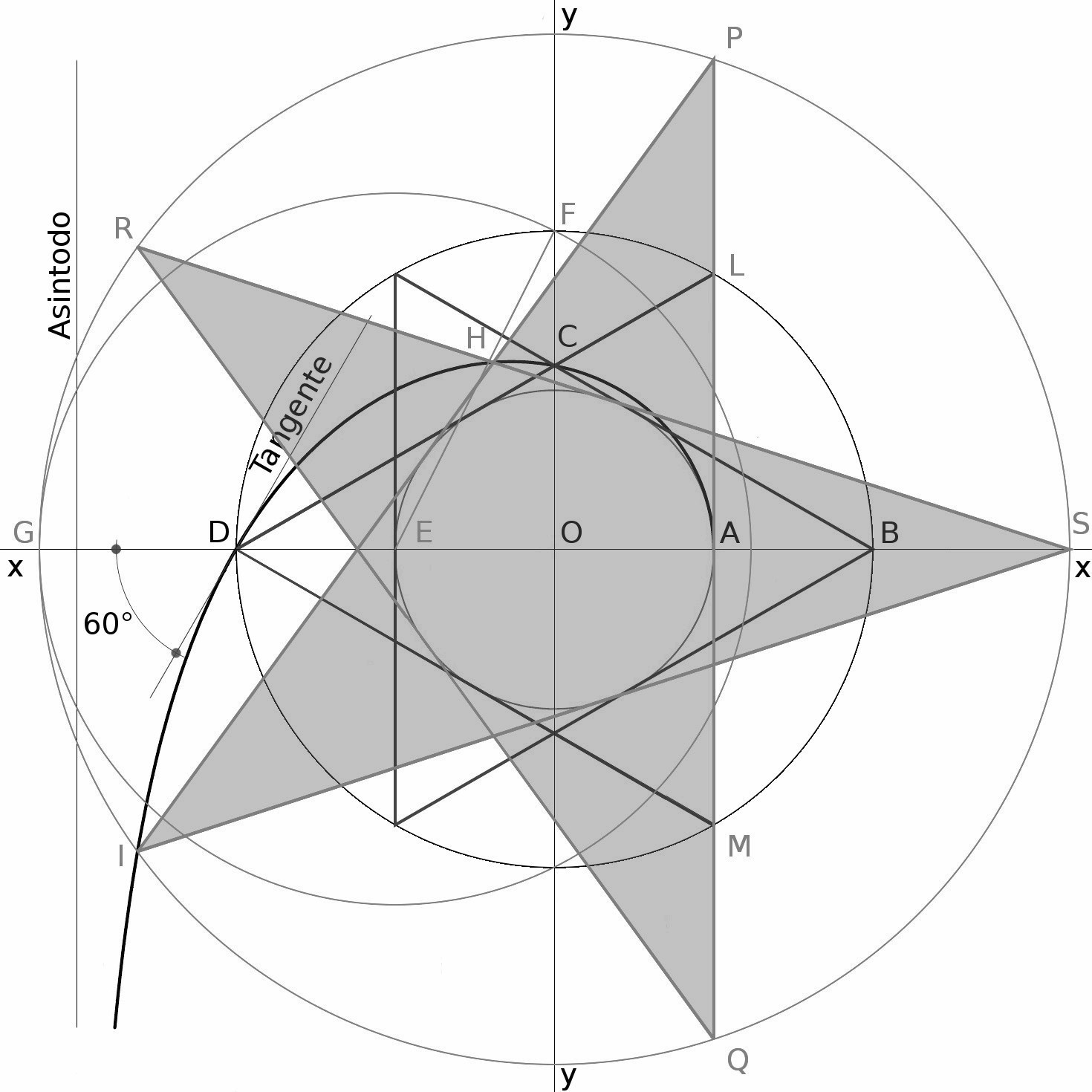
Il successivo caso, con l’illustr. 3, riguarda la curva del pentagramma che si ricava dal caso precedente dell’esagramma.

Non è difficile questa operazione grafica. Basta puntare col compasso in E, con raggio EF e tracciare un cerchio per rintracciare il punto G.

Successivamente si centra il compasso in O e si traccia il cerchio di raggio OD entro il quale si delinea il punto I sulla curva, di una delle punte del pentagramma ricercato. Di qui si comincia a tracciare la prima direttrice IP del pentagramma cui fanno seguito le successive, tutte tangenti al cerchio di raggio OE dell’esagramma.

Riesaminando la geometria della curva in osservazione in termini di geometria differenziale, essa può essere definita come una curva avente il seguente angolo δ variabile  fra il raggio (o vettore traiettoria) e il vettore tangenziale:

δ = arctan 3 cotan (θ / 3), dove θ è l’angolo tra il vettore traiettoria e il vettore iniziale della curva.

Ed ora si esamina il lato delle proprietà della curva in base al concetto cosiddetto dei limiti.

In matematica, il concetto di limite serve a descrivere l’andamento di una funzione all’avvicinarsi del suo argomento a un dato valore oppure l’andamento di una successione al crescere illimitato dell’indice. I limiti si utilizzano in tutti i rami dell’analisi matematica; sono usati ad esempio per definire la continuità, la derivazione e l’integrazione. Il concetto di limite di una funzione, più generale del limite di una successione, può essere generalizzato da quello di limite di un filtro.(2)

Si capisce che si tratta di un lato della questione matematica sulla curva in esame che comporta l’intervento di un matematico specialista di questo lato matematico, ed io con la limitazione di dilettante non sono idoneo ad espletarla come si conviene. Ma non potendo disporre dell’aiuto suddetto cercherò di dare una spiegazione, poi giudicherà il lettore matematico se ho colto nel segno o no.

Dunque:

Per θ = 180°,  cos (θ / 3) = 0

Ora si tratta di risolvere la formula

ρ = ρ0 / cos (θ / 3)

cioè di un numero fratto 0

Ma un numero diviso zero è un’operazione che in Matematica non è definita, cioè non ha senso dividere un numero per zero.

Capire il motivo per cui la divisione per zero è un’operazione priva di significato è semplicissimo: la divisione è l’operazione inversa della moltiplicazione così, ad esempio,

8 : 4 = 2

perché 2 è quel numero che moltiplicato per 4 dà come risultato 8.

Se cerchiamo di calcolare un numero diviso zero ecco cosa succede:

8:0 = a quel numero che moltiplicato per 0 ci dà 8 ma, come ben sappiamo, qualsiasi numero moltiplicato per zero dà 0, quindi è impossibile ottenere 8.

Ecco così spiegato perché non ha senso calcolare un numero diviso zero.

Ha senso invece parlare di numero diviso zero coi limiti.

Parlare di numero fratto zero ha senso solo nell’ambito dell’Algebra di infiniti e infinitesimi e, come vedremo tra poco, non è corretto dire che un numero fratto zero dà infinito.

Innanzitutto dovrebbe essere chiaro che non ha senso calcolare un numero diviso zero ma al più ci si potrebbe chiedere quanto vale

(lim/𝑥→0) 𝑎/𝑥

dove 𝑎 è un qualsiasi numero reale.

In realtà nella scrittura precedente si dovrebbe specificare se x tende a zero da destra o a zero da sinistra e quindi calcolare

(lim/𝑥→0+) 𝑎/𝑥 ; (lim/𝑥→0-) 𝑎/𝑥

Ancora, il risultato di questi due limiti dipende dal numeratore che potrebbe essere un numero positivo, negativo o nullo. In definitiva, il valore di un numero fratto zero varia a seconda del caso che ci si presenta dinanzi.

1) Numero positivo fratto zero

Se a è un numero maggiore di zero 𝑎>0  allora

(lim/𝑥→0+) 𝑎/𝑥 = +∞ ; (lim/𝑥→0-) 𝑎/𝑥 = -∞

2) Numero negativo fratto zero

Se 𝑎 è un numero minore di zero 𝑎<0 avremo che

(lim/𝑥→0+) 𝑎/𝑥 = -∞ ; (lim/𝑥→0-) 𝑎/𝑥 = +∞

Vedi numero-fratto-zero.html
Ed ora va esaminata la questione della relazione dell’asse verticale della curva con quello dell’asintodo che sono paralleli. Ma la “legge” in proposito porta a dire che:

«Due rette che scorrono parallele tra loro non potranno mai incontrarsi se non all’infinito»

Significa che due rette parallele hanno la possibilità di incontrarsi, ma solo se si attribuisce loro dei valori infiniti.

A questo punto in derivazione del fatto che le due rette, dell’asintoto e dell’asse y della curva, si incontrano all’infinito, il vettore ρ = ∞,

cosa che trova la conferma nel ragionamento appena fatto nell’ambito dell’Algebra di infiniti e infinitesimi.

Cosa porta a suggerire questa condizione, in cui il cerchio di raggio ρ0 = 0  e ρ = ∞ ?

Suggerisce una meravigliosa concezione filosofica sul cerchio.

Immaginando che siano infiniti i raggi ρ,  allora il centro con ρ0 = 0 corrisponde all’uomo e il cerchio con raggio ρ = ∞ corrisponde a Dio.

In conclusione la sorte della curva in esame, comunque, sembra appesa un tenuo filo, a causa del fatto che il mio ragionamento sui limiti merita l’approvazione di vero matematico, se non fosse per il soccorso di una curiosa galassia diversa dalle solite e per giunta la più grande mai vista dagli astrofisici fino ad oggi, la galassia NGC 8672, che sembra essere una doppia curva uguale quella di incerta concezione matematica. Ma è solo l’inizio di molti altri soccorsi sul filo del genere di nessi non matematici.

Una doppia curva dei poligoni stellati nella galassia NGC 6872?

La magia dei numeri di Fibonacci e del loro rapporto aureo, con la spirale logaritmica, sembra avere il dominio indisturbato della natura della Terra. Si manifesta nei cristalli, nelle conchiglie, nei cavolfiori, negli ananas, nel volo del falco pellegrino, nel corpo umano, negli uragani.

Ma è un’espansione che va oltre il nostro mondo. La spirale logaritmica, costruita è riscontrabile nell’Universo e dona la forma a diversi tipi di galassie. Ma ve n’è una che vi si discosta da questa forma, come la galassia NGC 6872, che è qualcosa di nuovo e sorprendente, persino nel nome di curva e non spirale.

La sua forma sembra trovare aderenza, appunto nella curva dei poligoni stellati regolari appena esaminata in modo matematico, come si può costatare dall’illustr. 4. A detta degli astrofisici, la NGC 6872 è la più grande galassia oggi nota.

Questa galassia rientra nella categoria delle Galassie irregolari che non hanno una forma ben definita (fino a questo momento) ed è nota come galassia a spirale barrata NGC 6872. È stata osservata il 29 marzo 1999, dall’European Southern Observatory (ESO). La sua forma è stata interpretata col segno matematico di integrale. Questa galassia è di tipo SB (s) b ed è accompagnata da una galassia più piccola, che interagisce con lei, la IC 4970 che è di tipo E7-S0.

I dati astronomici della NGC 6872 sono:

(epoca J2000)

Costellazione Pavone

Ascensione retta 20h 16m 56,5s/20h 16m 57,1s

Declinazione  -70° 46′ 06″/-70° 44′ 58″

Distanza 220 milioni di anni luce

Mi viene di dire sorridendo, alla luce della curva dei poligoni stellati, la galassia NGC 6872 può mai essere considerata irregolare, sol perché non ha la forma della spirale logaritmica come tante altre, alla luce di un’interessante curva geometrica che le si confà?

Intanto risalta evidente il fatto che la mia curva, giustificherebbe la forma della galassia NGC 6872. E qui niente ci piove. Ma una cosa che diventa interessante per questa galassia, è il lato delle proprietà matematiche della curva geometrica da me concepita, che vi corrispondono. Aggiungendo poi il fatto che è stata ritenuta la più grande mai rilevata, di dimensioni quattro o cinque volte maggiori della nostra Via Lattea, oltre ad essere la più grande galassia di tutto il cosmo, allora le tre cose fanno scalpore, secondo me.

Il primo fatto matematico singolare della curva in questione è che essa è generatrice di tutti i poligoni regolari stellati. Di qui il concetto traslato alla miriade di stelle che la compongono. Ma questo è un segno che non incide sulla razionalità scientifica.

Ma desta interesse, per esempio, la barra delle galassie a “barra sbarrata” dal cui bulbo centrale si dipartono due prolungamenti di stelle che nell’insieme ricordano una barra, appunto, e nella doppia curva geometrica è la stessa che la unisce alla seconda curva gemella. In queste galassie i bracci curvi della spirale partono dalla barra, anziché dal nucleo. Si usa anche il più generico “galassia barrata”, in quanto la barra è presente anche in galassie di diversa morfologia.

E ancora.

Cosa implica  in più tutto ciò? Implica che per la doppia curva, volendo esprimere – mettiamo – il concetto di Dio (perché sin dall’inizio è qui il nodo gordiano posto nell’articolo di Matteo  Matzuzzi di Il Foglio.it) il cerchio all’infinito rappresenta Dio e l’origine delle due curve, l’Umanità. Cosa nota per la definizione del cerchio con i due enti, il cerchio e il punto, che però sono lontani fra loro, dunque irraggiungibili. Il raggio poi è un terzo ente che è immaginario, mentre per la curva, è la stessa che diventa al limite una retta, li unisce. Ed è la condizione di tutti i mistici del cristianesimo che realizzano in loro l’unità con il Signore Cristo Gesù. E c’è di più, perché si può immaginare che le curve rettificate sono infinite e sono costellate da infiniti stelle-universi per formare l’intero cosmo.

La galassia NGC 6872, dal canto suo, è stata battezzata col nome di “integrale” per la sua forma, (illustr. 5) e questo già combacia alle proprietà della curva in questione. Infatti in analisi matematica, l’integrale è un operatore che, nel caso di una funzione di una sola variabile a valori reali non negativi, associa alla funzione l’area sottesa dal suo grafico entro un dato intervallo [a, b] nel dominio. Se la funzione assume anche valori negativi, allora l’integrale può essere interpretata geometricamente come l’area orientata sottesa dal grafico della funzione. E se l’intervallo è fra zero e infinito allora la relazione al limite è perfetta. Tuttavia, cogliendo la mia concezione spirituale di Dio e l’Umanità, da un lato, e dall’altro il fatto che la NGC 6872 è (per ora) la più grande galassia mai osservata, allora ben si addice – mettiamo – DIO È CON NOI. O qualsivoglia altra definizione simile, e non un creatore che poi scompare per lasciare nel buio le sue creature.

Di qui la conferma alla conclusione della risposta che si dà l’astrofisico Marco Bersanelli , di cui all’inizio:

La creazione non è relegata al Big bang, a quel momento in un lontanissimo passato. La creazione avviene sempre, anche ora”. Perché DIO È CON NOI, attimo dopo attimo.

Ma c’è voluta una curva geometrica, e quella di una galassia, la NGC 6872, la più grande fin’ora avvistata, di un lungimirante dilettante di matematica che, col suo minuscolo telescopio interiore, l’ha avvistata… Per ora, ma segue la natura che in molti casi si è conformata alla curva “Integrale”, chiamiamola così in mancanza di altri nomi. È valsa per la galassia NGC 6872 per bocca degli astrofisici e vada anche per la curva che la informa.

La curva “Integrale” in natura

«Osservate come crescono i gigli del campo: non lavorano e non filano. Eppure io vi dico che neanche Salomone, con tutta la sua gloria, vestiva come uno di loro. Ora se Dio veste così l’erba del campo, che oggi c’è e domani verrà gettata nel forno, non farà assai più per voi, gente di poca fede?» (Mt 6, 28-30).

I gigli del campo fanno parte di un discorso tenuto da Gesù e riportato nel vangelo di Matteo e nel vangelo di Luca. Il discorso riporta diversi riferimenti al mondo naturale: sono menzionati gli uccelli, i gigli e le falene. Dunque non meraviglia riscontrare in molti casi, nella conformazione di molti vegetali, come i cavolfiori, gli ananas, le pigne note come stroboli, i fiori ed ancora con tanti altri esempi, la firma del creatore Iddio, e tramite chi? Se ne è parlato in precedenza: con la matematica, con la magia dei numeri di Fibonacci e del loro rapporto aureo, la spirale logaritmica. Ma solo in tal modo? No, perché anche la curva “Integrale” ha le sue creature del mondo della natura, solo che vanno viste componenti di un solidi e non di un piano.

Le cactacee cioè i cactus rappresentano più di altri vegetali la curva “Integrale”, di cui il Cereus giganteus dell’illustr. 6. Sono piante succulente (piante xerofite, adattate agli ambienti aridi mediante l’accumulo di acqua all’interno di tessuti succulenti) che comprende circa 3000 specie e 120 generi.

A causa delle spine, moltissima gente quasi le detesta, tuttavia esistono moltissime associazioni di amatori di soli cactus (nella Nuova Galles del Sud come a Vienna, a Praga, a Tokyo, a Mosca, a Zurigo e, naturalmente, a Città del Messico).

Non si spiega perché, ma è una pianta dalle misteriose origini che, per quanto delle piante grasse rimangano pochissimi fossili che ci parlino della loro storia, ne è stato ritrovato uno di una strana pianta, molto simile a una moderna Consolea, negli Stati Uniti, nell’Utah, nei terreni risalenti all’Eocene e datati approssimativamente tra i 50 e i 35 milioni di anni fa. È stata denominata Eopuntia, ed è l’unica traccia che ci permette di risalire a un’epoca precedente le quattro grandi glaciazioni, che videro la comparsa e l’evoluzione dell’uomo, e ci pone il grande interrogativo di quali siano stati i rivolgimenti della crosta terrestre che hanno determinato adattamenti cosi diversi in piante che hanno mantenuto inalterati i caratteri botanici.(3)  Sembra quasi un parallelo alla lontanissima galassia NCG 6872 – mi viene da dire -, non che ci sia una ragione ben precisa in merito. Non mancano molti altri esempi di piante o i loro frutti, per esempio l’ananas che si vede nell’illustr. 7.

L’ananas (Ananas sativus), il re della frutta.  La pianta su cui cresce è l’ananasso che appartenente alla famiglia delle Bromeliacee. Originario delle zone del Sud America e conosciuto fin dall’antichità dalle popolazioni come i Maya e gli Atzechi, fino ad essere importato in Europa da Cristoforo Colombo e attualmente è diffuso in tutto il mondo. Ma questo frutto si differenzia per la conformazione dal cactus per la trama esteriore, visibilmente legata alla curva “Integrale”.

Se nel cactus la curva scorre verticalmente in modo lineare, nel cactus si sviluppa in modo avvolgente. Potendola vedere dall’alto la trama delle spire avvolgenti si sviluppa secondo la spirale logaritmica o aurea. Questa condizione la si riscontra in molti altri casi come la pigna nota col nome di strobolo. Un’altro caso simile al cactus, per la trama delle curve “Integrale”, è quella delle zucchine.

Il panorama dei vegetali ci permette di immaginare che il cielo delle galassie, con le diffuse conformazioni a spirale cui si aggiunge la  galassia NCG 6872 a forma di curva molto diversa, quasi si riflette sulla terra, chissà assumendo ognuna di loro, la paternità di determinati vegetali.

Viene da meditare sul conto dei vegetali, quasi baciati dal cielo delle lontanissime galassie con le loro stelle, come se in modo capovolto questi immaginari baci si diramino in altrettante immaginabili radici da cui traggono la linfa vitale le piante, e con loro l’uomo stesso da cui trae alimento. Per esempio, traslando questo concetto quasi fanciullesco, nella matematica e particolarmente alla curva che ho chiamato “Integrale”, come la galassia NCG 6872 che le somiglia moltissimo. Effettivamente sembra un gambo con fiori sospesi di ogni tipo al posto dei poligoni stellati che richiamano le stelle del cielo notturno. E già questo esempio ci porta all’idea di un albero le cui radici sono così profonde da raggiungere l’infinito. Ed ecco che si illumina la parabola evangelica citata all’inizio di questo capitolo:

«Osservate come crescono i gigli del campo: non lavorano e non filano. Eppure io vi dico che neanche Salomone, con tutta la sua gloria, vestiva come uno di loro. Ora se Dio veste così l’erba del campo, che oggi c’è e domani verrà gettata nel forno, non farà assai più per voi, gente di poca fede?» (Mt 6,28-30).

Ed ancora per aggiungere valenza al mondo delle piante vale esaminare i seguenti primi 3 versetti del capitolo 7 dell’Apocalisse di Giovanni in cui è coinvolta la sorte del mondo delle piante.

«1. Dopo questo vidi quattro angeli, che stavano ai quattro angoli della terra e trattenevano i quattro venti, perché non soffiasse vento sulla terra, né sul mare, né su alcuna pianta.
2. E vidi salire dall’oriente un altro angelo, con il sigillo del Dio vivente. E gridò a gran voce ai quattro angeli, ai quali era stato concesso di devastare la terra e il mare: 3. “Non devastate la terra né il mare né le piante, finché non avremo impresso il sigillo sulla fronte dei servi del nostro Dio”.»

L’evangelista Giovanni ricorre a un modo brillante per far capire la relazione del mondo delle piante con i «servi del nostro Dio» che ricevono il sigillo sulla fronte, per citare il testo dell’Apocalisse. Si tratta del segno che fa capire la salvezza degli israeliti segnati dal sigillo, perché il mondo delle piante che vi si lega, si salva dalle devastazioni operata dai quattro angeli.

Il punto è questo, sintetizzando: i quattro angeli, al di là di trattenere i quattro venti, in modo da impedire che agiscano sulla terra, mare e piante, hanno il potere di far riversare il vento devastatore sulla terra e il mare, ma non sulle piante.

E fin qui si capisce che il mondo delle piante è fuori pericolo dalla devastazione, ma che senso ha l’aver dato ordine, da parte del quinto angelo, di devastare, dopo la fase del sigillo sulla fronte agli israeliti, terra, mare e piante se i tre angeli della devastazione avevano di mira solo i mondi della terra e del mare? L’unica ragione di questa ambiguità è di far capire in modo velato una doppia cosa, la salvezza di entrambi, e questa non desta perplessità, ma l’altra sì, ossia la loro relazione.

Il mio pensiero mi porta alle due piante al centro del paradiso dell’Eden. Con l’albero della scienza del bene e del male ebbero relazione Adamo ed Eva e da qui ci fu la disgrazia; resta l’albero della conoscenza con il quale l’uomo della salvezza avrà relazione nel futuro. Ed è per questa ragione che il mondo delle piante si salva, come fa capire Giovanni nell’Apocalisse.

Ma l’albero della salvezza al suo rivelarsi, nel racconto della Bibbia porta ad un altro mistero da risolvere. Si tratta di tre versetti del libro Genesi che destano perplessità e sono causa di inciampo per molti credenti e sono questi:

1. Gn 2,9 – «Il Signore Dio fece germogliare dal suolo ogni sorta di alberi graditi alla vista e buoni da mangiare, e l’albero della vita in mezzo al giardino e l’albero della conoscenza del bene e del male.»
2. Gn 2,17 – «Tu potrai mangiare di tutti gli alberi del giardino, ma dell’albero della conoscenza del bene e del male non devi mangiare, perché, quando tu ne mangiassi, certamente moriresti.»
3. Gn 3,2-3 – Rispose la donna al serpente: «Dei frutti degli alberi del giardino noi possiamo mangiare, ma del frutto dell’albero che sta in mezzo al giardino Dio ha detto: Non ne dovete mangiare e non lo dovete toccare, altrimenti morirete».

Il fatto che desta perplessità è nei due alberi che stanno allo stesso posto, in mezzo al giardino edenico, per cui, ammesso che stiano uno accanto all’altro, com’è che nella Bibbia non si parla di Eva che non vede l’albero della vita e i relativi possibili frutti, ma solo l’altro del male e del bene e il serpente? Come si spiega?

La possibile ambiguità sta nel fatto che in Adamo ed Eva dovette cominciare a germogliare in loro l’Ego, perché solo in tale stato la loro vista, da che era teocentrica dovette iniziare a offuscarsi e in conseguenza il serpente dell’albero apparì a loro e li tentò, come in effetti è riportato nella Bibbia. Ma la spiegazione di questa versione sta in piedi al momento in cui Iddio crea Adamo con la compagna Eva. E tutto si fa chiaro se si torna indietro nel tempo allorché fu creato il primo Adamo, quando Iddio si rese conto che era solo. In effetti non era proprio tanto solo perché Eva era in lui ed essere una creatura ermafrodita. Eva era in lui attraverso la costola che valse poi l’atto formale per far nascere Eva accanto ad Adamo in seguito. Per conseguenza, solo a queste condizioni si delineò in loro l’Ego che prima era unito in Adamo, come due serpenti uniti in amore. E da qui cominciarono a nascere le incertezze dei due. L’Ego è la finestra dove si profila il serpente in noi e occorre riunirlo con la parte mancante con forza e determinazione per ripristinare lo stato del primo Adamo (cosiddetto androgino). I due, l’Ego e l’Io rivolto a Dio, sono in noi e vanno riuniti. L’esperimento pratico di questo stato è possibile farlo con una barretta di calamita. Unita com’è funziona a meraviglia ma se la spezziamo diventano due calamite indipendendenti fra loro, così come possono essere una coppia di un uomo e una donna. Ma se si tenta di riunirle è cosa vana, non si riattaccano e si respingono fra loro, la dov’è stata spezzata in due. Il campo di battaglia dei mistici è la sfrenata lotta col serpente Ego (la repulsione delle due calamite spezzate) fino a che si profila in loro la luce di Dio che li solleva dallo stato, quasi mortale, in cui si riducono in seguito alla lotta. Ma in altro modo va vista questa lotta e ce la presenta la stessa Bibbia con la lotta di Giacobbe.

Il libro della Genesi racconta nel trentaduesimo capitolo:

«E Giacobbe si alzò quella notte, prese entrambe le sue mogli, entrambe le sue ancelle e i suoi dodici figli e li condusse oltre il guado dello Iabbok. Li prese e li portò al di là del fiume e portò tutto ciò che aveva. Giacobbe rimase indietro da solo. Qui un uomo lottò con lui fino all’aurora. Quando vide che non riusciva a vincerlo, gli toccò il fianco. Così il fianco di Giacobbe si era lussato mentre combatteva con lui. E disse: “Lasciami andare! L’aurora sta risuonando!”. Disse: “Non ti lascio finché non mi benedici!” Gli disse: “Come ti chiami?” Egli rispose: “Giacobbe”. Lui disse: “D’ora in avanti non ti devi chiamare Giacobbe, ma Israel. Hai lottato con Dio e con gli uomini e hai riportato la vittoria”. Quindi Giacobbe fece questa richiesta: “Rendi noto il tuo nome!”. Egli disse: “Che cosa mi chiedi del mio nome?” Allora lo benedisse. E Giacobbe chiamò il luogo Penuel: “Ho guardato Dio faccia a faccia e sono rimasto in vita!”. E il sole si alzò…» (Genesi 32, 23-33).

L’avvenimento è misterioso. Affonda nella memoria e vi rimane impresso. Forse non lo si capisce, oppure si sente che è pieno della realtà più sacra. Ci si riflette, lo si tira fuori e vi si trova sempre ancora qualcosa in più.

Giacobbe torna nella sua patria, dopo che è rimasto a lungo all’estero. Lì riceve la notizia dell’arrivo di suo fratello Esaù ingannato per il suo diritto di primogenitura e per la benedizione paterna. Giacobbe ha paura, manda via i suoi familiari… rimane tuttavia li da solo nella notte. Sente che qualcosa si avvicina. Allora — la Scrittura racconta, come raccontano le vecchie saghe, senza passaggi intermedi, con sequenze messe in contrappunto — “un uomo combattè con lui fino alla comparsa dell’aurora“.

«L’uomo» è quell’essere che spesso ritorna nella Genesi: l’”angelo del Signore“. In questa forma si entra misteriosamente: a volte sembra essere una creatura, a volte sembra Dio stesso e alcuni pensano che sia il Figlio. Si imbatte in Giacobbe e lotta con lui, che comunque resiste. La lotta è meravigliosa: l’uomo non riesce a sconfiggerlo, ma basta che gli tocchi l’anca ed è lussata. Un’oscura penetrazione di predominio e di debolezza nello stesso tempo. Giacobbe rimane il vincitore. La ricompensa della lotta è però un nuovo nome e la benedizione di questo da parte dell’uomo. E in seguito “il sole si alza“.

Questo è successo a Giacobbe. Era uno di quelle grandi figure, gli uomini erano pieni di forza terrena e comunque trattavano con Dio. Potenti in terra, della realtà più densa e nello stesso tempo circondati dal mistero di Dio. Egli era un eletto; a lui viene rivelato qualcosa che vale per tutti noi.»(4)

E il cerchio si chiude per mostrare una certa immagine dell’antico doppio serpente in amore nella galassia NCG 6872. Sembra persino di notare nell’immagine di questa galassia (l’illustr. 4) episodio biblico dell’anca lussata causata dalla galassia accanto la IC 4970 (contenente un buco nero). Infatti una delle due curve sembra compromessa.

Brescia, 10 maggio 2021

---

1 Stephen-Hawking-era-tormentato-dalle-domande-radicali-dall-esistenza-di-dio
2 wikipedia.org/wiki/Limite_(matematica)
3 piante-grasse-cactacee-regole-generali-coltivazione
4 la-lotta-di-Giacobbe