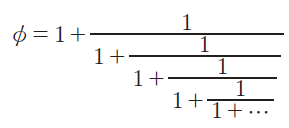Continuiamo ad analizzare quegli strumenti matematici che ci possono essere di aiuto nello studio e nella descrizione della Terra piatta. ɸ è il numero aureo che ho introdotto nell’articolo precedente. Possiamo affermare che una linea è divisa in base alla sezione aurea quando possiamo trovare questa proporzione: AB/AC=AC/CB
Quando questi segmenti rispettano la suddetta proporzione, il rapporto AC / CB corrisponderà a 1,6180339887 … Euclide è stato il primo a descrivere questa cifra, che è anche conosciuta come il numero aureo o sezione aurea. ɸ, come π, è un numero irrazionale e non può quindi essere descritto da una frazione di numeri interi. Euclide descrisse questo rapporto solo per scopi geometrici; probabilmente non immaginava che questo numero potesse avere conseguenze importanti in campi molto diversi. Si pensi ad esempio alla descrizione della disposizione delle foglie su un albero o alla descrizione delle galassie in astronomia.
Esattamente come il Pi Greco, ɸ può essere espresso come una somma di molti elementi, uno più grande sommato a molti altri frattali meno importanti ma che ripetono il corpo principale. Questo modo di descrivere le cose, con un corpo principale, più frattali simili si rivelerà essere molto importante nella descrizione delle misure della Terra. Un modo per esprimerlo è:
È interessante il fatto che, come si può dedurre da questa equazione, ɸ si ottiene da una serie di frazioni con molti uno ripetuti. Mostrerò in un ulteriore capitolo che, nel descrivere la Terra, le cifre ripetute appaiono molte e molte volte. Ho già evidenziato il collegamento tra la sezione aurea e il numero 72 ma, riguardo a questo argomento, voglio aggiungere qualcosa di veramente interessante.
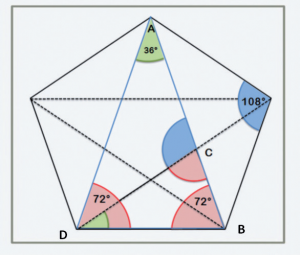
72 ° è la quinta parte del cerchio: 360 ° / 72 = 5 e in realtà esiste un collegamento tra ɸ e il pentagono. Disegniamo un pentagono inscritto in un cerchio. Si disegnino quindi due diagonali del pentagono, dividendo così il pentagono in tre triangoli. La stella che risulta entro il pentagono è chiamata pentacolo.
Il rapporto tra la diagonale e il lato del pentagono AB / BD è di nuovo pari alla sezione aurea. Ma quando dividi l’angolo di 72 ° con un segmento in due parti uguali, si troverà il punto C e, di nuovo, si ottiene AC / CB = ɸ.
Sorprendente è il fatto che ɸ è anche in relazione con il numero 666. Posso scrivere –2 ∙ sin666 = ɸ. Il legame tra sezione aurea, misure della Terra e numero della Bestia dell’Apocalisse risulterà chiaro più in la, ma qui voglio sottolineare il legame tra numero aureo e numeri a cifre ripetute come il 111 o il 666. Questo concetto si rivelerà essere importante, ma procediamo per passi.
ɸ può essere razionalizzato usando le serie Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 … Consideriamo, infatti, il rapporto tra numeri contigui della serie di Fibonacci, andando a crescere lungo tale serie:
1/1=1,000000
2/1=2,000000
3/2=1,500000
5/3=1,666000
8/5=1,600000
13/8=1,625000
21/13=1,615385
34/21=1,619048
55/34=1,617647
89/55=1,618182
144/89=1,617978
233/144=1,618056
377/233=1,618026
610/377=1,618037
987/610=1,618033
Questi rapporti si avvicinano sempre più alla sezione aurea e questo sorprendente fenomeno è stato scoperto da Keplero, l’astronomo. La serie di Fibonacci ha una bellissima proprietà collegata al numero 11, essendo l’undici ancora una volta un numero con cifre ripetute. Se sommi dieci numeri della serie, il risultato è sempre perfettamente divisibile per undici. Il risultato della divisione è sempre il settimo numero della divisione. Per esempio
1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 = 143
143/11 = 13
Una prova del fatto che la serie Fibonacci si rivela adatta alla descrizione della Terra, si ha dalla botanica. Si consideri la fillotassi, cioè la disposizione delle foglie sulle piante. Sugli alberi, foglie e rami sono disposti per massimizzare l’esposizione al sole. Sugli alberi di tiglio, le foglie sono ordinate su due lati opposti, essendo il coefficiente di fillotassi ½ che significa che, con un giro attorno allo stelo, ci sono due foglie o rami. Il faggio ha un coefficiente 1/3, il melo 2/5 mentre ci sono casi di alberi con un coefficiente 3/8. Tutti questi rapporti sono realizzati con termini vicini della serie Fibonacci, il cui rapporto è una razionalizzazione del numero aureo.
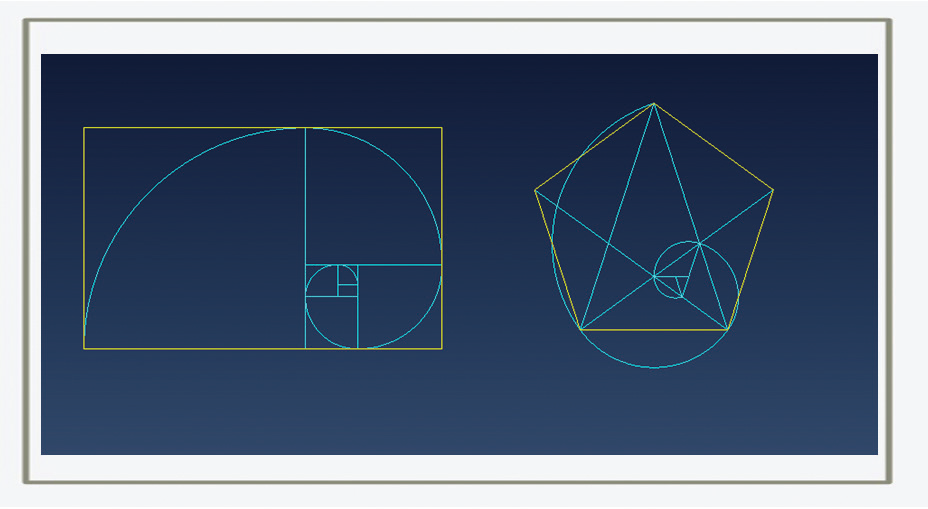
Fibonacci è il legame tra il numero aureo e i frattali, essendo entrambi strumenti matematici perfetti per descrivere la natura della realtà. Consideriamo ora la spirale logaritmica. Può essere ottenuta da una serie di rettangoli aurei, uno dentro l’altro. Si ottengono sottraendo un quadrato al rettangolo, come si può vedere nella figura seguente. Un rettangolo aureo ha la proprietà che il rapporto tra i lati è pari alla sezione aurea. La stessa spirale può essere ottenuta da un triangolo aureo, quello con un angolo di 72 ° all’interno.
Questa spirale ha una proprietà particolare: mentre cresce non cambia forma. Questa proprietà si chiama auto-somiglianza o auto-similarità ed è la stessa che possiamo trovare nei frattali: parti dei frattali sono simili al totale. Questa è esattamente la proprietà richiesta da molti fenomeni di crescita naturale. Si pensi ad esempio al Nautilus, che costruisce stanze sempre più grandi. Mentre il guscio aumenta, il raggio aumenta proporzionalmente. Di conseguenza, la forma generale rimane sempre la stessa. Si potrebbe dire: «Eadem mutato resurgo». Esistono molte forme naturali simili alla spirale logaritmica e molti astronomi collegano la forma delle galassie alla spirale aurea.
Infine, visto che siamo sul pezzo, potremmo prendere in considerazione la legge di Newton sulla gravità. La legge di gravitazione universale afferma che, raddoppiando la distanza, la forza di attrazione diminuisce, secondo un fattore 4. Questo perché la forza diminuisce con il quadrato della distanza. A causa di questa legge, in un sistema globulare, si presume che le orbite dei pianeti attorno al sole abbiano una forma ellittica. Ma supponiamo che la forza di attrazione possa diminuire di un fattore 8, anziché di 4.
Quindi, se, per caso, la distanza raddoppiasse, si dovrebbe immaginare un universo totalmente diverso. Quando la gravità diminuisce in base al cubo della distanza, le orbite dei pianeti diventeranno di conseguenza spirali logaritmiche. Di conseguenza, la Terra collasserebbe o si allontanerebbe dal sole. Le leggi di Newton, ovviamente, non agiscono in armonia con la matematica della Terra piatta.
Armonia e proporzioni sono, ovviamente, anche gli elementi base della musica. Sembra ben noto il fatto che la sequenza numerica di Fibonacci e il relativo “rapporto aureo” si manifestino in molte opere d’arte. Questi numeri sono anche alla base di determinati intervalli e composizioni musicali. La sequenza di Fibonacci è evidente nella struttura musicale della scala di ottava. Inoltre il più grande dei liutai, Stradivari, ha progettato i suoi violini attorno al rapporto aureo.
Pertanto, quando ci si avvicina all’arte, si può facilmente scoprire che la teoria delle proporzioni deve essere considerata la base razionale per la bellezza. E, insieme a questo, la matematica viene esaltata come base di molte diverse attività artistiche e principalmente della musica.
Questa estetica delle proporzioni, pur unendo grazia e bellezza, mi fa ricordare un verso di Giobbe. Si riferisce al Leviatano e recita: non nasconderò le sue parti, né il suo potere, né la sua proporzione gentile (Giobbe 41:12) Bibbia di Re Giacomo. Il Leviatano è, nel libro di Giobbe, una rappresentazione poetica della volta celeste. D’altra parte, Behemoth è una rappresentazione della Terra. Le loro proporzioni sono regolate secondo una matematica estremamente raffinata ed estetica: numeri della grande gioia o unità ripetute, come 111 o 666; o anche numeri irrazionali, come Pi o ɸ. E, naturalmente, l’auto-somiglianza e i frattali sono alla base di tutti questi calcoli.
Riporto di seguito un video sui numeri di Harshad. Assieme a sezione aurea e numeri di Demlo ci permetteranno di trovare le misure della Terra e costruirne un modello valido.
 Michele Vassallo è un ingegnere meccanico. Nel 2015, quando scoprì il movimento emergente degli American Flat Earthers, si sentì stupito e affascinato. Presto si rese conto che la Terra non poteva essere un globo. Nonostante il fatto che gli argomenti venuti alla ribalta fossero e siano ancora incompleti e contengano molti errori, il concetto generale di una terra piatta sembra assolutamente degno di indagine.
Michele Vassallo è un ingegnere meccanico. Nel 2015, quando scoprì il movimento emergente degli American Flat Earthers, si sentì stupito e affascinato. Presto si rese conto che la Terra non poteva essere un globo. Nonostante il fatto che gli argomenti venuti alla ribalta fossero e siano ancora incompleti e contengano molti errori, il concetto generale di una terra piatta sembra assolutamente degno di indagine.
Tra le sue migliori scoperte c’è la reintroduzione dell’etere nella fisica della terra piatta e una nuova visione della natura della luce.
E’ coautore del libro “The real measures of the (flat) Earth” edito da Aracne editore e del blog “rifugiatidipella.com“. Dal 2019 produce materiale video inerente la Terra piatta sul suo canale Youtube “earthmeasured”.